1- 9p

临界表面张力研究

资料来源；染整工程第四册p133-148陶乃杰主编

当一个小水滴置于光滑均匀的固体表面上，由于液体和固体的表面张力 (分别用Y_LG和Y_SG表示)，以及液-固间的界面张力 (Y_LS)相互作用的结果，决定了液滴铺展的情况(从圆珠形到完全铺平)。除液体在固体表面迅速渗开而将固体完全润湿外，液滴在固体表面上处于平衡状态时如图4-1所示。

通过水滴与固体平面的接触点A作水滴的切线，该切线与固体平面间的夹角称接触角θ，其与液、固表面张力的关系如杨氏方

程式所示，

当θ=0°时，液滴在固体表面完全铺平，表示固体表面被液滴完全润湿，当θ= 180°时，液滴为圆珠形，这是一种理想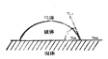

图4-1 液滴在固体面的平衡状态

的不润湿状态；当θ=90°时，表示固体已有拒水效果。在拒水整理中，可将液体 (水)的表面张力看作是常数。因此，液体能否润湿固体表面，决定于固体的表面张力 (Y_SG)和液-固的界面张力 (Y_LS)。从拒水要求来说，Y_SG- Y_LS 应为负值，即θ＞90°。

液-固间相互作用是导致润湿性大小的原因，可用附着功W_A来表示。所谓附着功是指分离单位液-固接触面积所需之功，它是液-固界面结合能力及两相分子间相互作用力大小的表征；

W_A= Y_SG + Y_LG- Y_LS (2)

合并(1)和(2)式，则得:

W_A= Y_LG(1+cosθ) (3)

式(3)表明附着功是接触角θ的函数。附着功越大，润湿性越强；粘附功越小，拒水性越强。

当Y_SG = Y_LG， Y_LS =0 ， W_A=2Y_LG= Wc

则Wc为液体的内聚功(表示分离单位面积液柱所需之功)，那么当附着功(W_A)等于内聚功(W_C)时，接触角为零，这时液体在固体表面完全铺开。由于cosθ不能超过1，因此即使附着功大于2Y_LG (即W_A＞W_C，接触角仍保持零不变。如果W_A= Y_LG，则θ为90°，当接触角为180°时，W_A=0，表明液体和固体之间没有附着作用。然而由于两相间多少存在一些粘着作用，所以接触角一般为160°或更大一些。而不等于180°。

从上述讨论可知，当W_A≥W_C时，液体才能在固体表面铺展，以固一液界面代替固-气界面。当铺展面积为单位值时，体系自由能降低为；

-△G=S=W_A-W_C （4）

S为铺展系数，它与界面张力之间的关系可表示为，

S=Y_SD+Y_LG-Y_LS-2Y_LG=Y_SG-(Y_LS+Y_LG) (5)

在式(5)中，若S＞0，液体可以在固体表面自动展开，连续地从固体表面取代气体 (即润湿或渗透)；若S＜0，液体在固体表面不能铺展 (即成珠状)。由于式(5)中Y_LS与Y_LG相比，其值甚小，可忽略不计，因此，若要水对固体表面不润湿，则必须使固体表面张力（Y_SG）小于液体的表面张力（Y_LG）。

表面能低的固体平面不易被水所润温，但是缺乏有效的测定固体表面能的方法，大量集中于间接测定或通过与之成比例的量，表示没有定值。几十年来，随着高聚物的广泛应用，以及对低能表面润湿性的进一步研究，齐斯曼 （ZiSman）等发现，同系物液体在同一固体平面上的接触角随液体表面张力降低而变小。以其cosθ对液体表面张力作图，可得一直线，将直线延长至cosθ=1之处，相应的表面张力值称为此固体平面的临界表面张力，以Y_C表示。图4-2表示正烷烃同系物在聚四氟乙烯表面上的

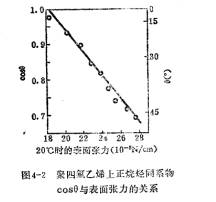
cosθ值与其相应的表面张力之间的关系，若将此直线外推至cosθ=1(即接触角为零)之处，得其相应的表面张力值约为 18×10^-5N/cm；此值即为该固体表面的临界表面张力。