测试与标准

纺织品禁用偶氮染料检测不确定度评估qt-081207-2

陈琳, 蔡国兴, 周强, 黄中权 江苏盛虹纺织品检测中心,江苏吴江215228

收稿日期: 2008-06-16

作者简介: 陈琳(1983-),女,江西高安人,硕士研究生,现从事生态纺织品的检测及研究工作。

原载：印染2008/16；35-38

网上来稿: zhanyizhen 08-8-7

【摘要】按照EN14362 - 2: 2003标准测定纺织品中可萃取的禁用偶氮染料,以4, 4′2 二氨基二苯甲烷为例,对该方法整个过程中产生的测量不确定度进行评估,通过对不确定度来源的分析、量化,合成了不确定度。结果表明,按本试验方法,禁用偶氮染料检测过程中随机效应是最大影响因素。

【关键词】测试; 禁用偶氮染料; 纺织品

【中图分类号】TS197　文献标识码: C　文章编号: 1000-4017(2008)16-0035-04

0　前言

随着各国生态环保要求的日益提高,纺织品禁用偶氮染料的检测已成为出口纺织品检测的一项重要内容。因检测结果不合格而发生退货的情况屡有发生,给各出口企业及生产厂家带来巨大的损失。因此,为了提高检测结果准确性,正确评估该项测试的不确定度很有必要。

ISO/IEC 17025[1]标准在“5.10.3C.”中规定,测试报告需有“评估测量不确定度的声明(适用时),如果不确定度与测试结果的有效性或应用有关,或客户说明中提出要求,或不确定度影响与规范限量的符合性时,则测试报告中需加入有关不确定度的信息。”测试结果包含不确定度信息后,可使测试结果的表达更科学、更完整。另外,通过对各不确定度分量的评估,可从中找出其最大分量,从而对产生这些分量的测试要素加以控制,以期获得更准确、更精确的测试结果。

1　测试方法

现以本实验室检出率较高的4,4′-二氨基二苯甲烷为例,采用EN14362-2:2003[2]检测方法,对纺织品禁用偶氮染料测定不确定度进行评估。

1. 1　试样制备

　　取代表性试样,剪成5mm×5mm碎片,混匀,准确称取1.00g(精确至0.01 g)置于反应器中。

1. 2　提取

在提取器中加入25mL氯苯,加热提取30min,提取液冷却至室温后,于50℃低真空蒸干。加入2mL甲醇,在超声振荡器中均匀分散,然后全部转移至反应器中。

1. 3　还原裂解

向反应器加15mL柠檬酸盐缓冲液,于(70±2)℃水浴中恒温振荡(30±2)min。加入3.0 mL连二亚硫酸钠溶液,剧烈振荡后立即放回(70±2)℃水浴中,还原(30±1)min,并在2min内冷却至室温。

1. 4　分离浓缩

萃取液完全滗入硅藻土柱中,吸附15min。然后用80mL叔丁基甲基醚按10、10、20、40 mL的顺序洗脱。洗脱液于50 ℃下真空浓缩至1mL。用缓氮气流吹干。

1. 5　定容测量

浓缩后残余物立即用2.0mL甲醇内标溶液溶解,过滤,用GC/MS定性,内标法定量。

1. 6　样品中胺含量的计算公式

W =	As ×AISS ×ρc ×V	(1)
	Ac ×AISC ×mE

式中: W ———样品中胺的含量,mg/kg;

As ———样品溶液中胺的峰面积;

Ac ———校正溶液中胺的峰面积;

AISS ——样品溶液中内标的峰面积;

AISC ——校正溶液中内标的峰面积;

Ρc —— 校正溶液中胺的浓度,μg/mL;

V ——— 最终样品的体积,mL;

mE —— 纺织品的质量, g。

2　不确定度来源分析

2. 1　样品质量引入的不确定度

其来源于三个方面:测量的重复性、读数的分辨率和天平校准的不确定度。

2. 2　提取产生的不确定度

主要是移液体积引起的不确定度,但由于移液体积偏差很小,且提取后溶液需蒸干,故可忽略。而加热、旋转蒸发、超声分散及溶液转移过程中产生的是随机效应,因而各因素对不确定度的影响也是随机的,其不确定度应包括在A类不确定度中。

2. 3　还原裂解产生的不确定度

由于15mL缓冲液是反应介质,介质浓度和体积上的微小差别对测量结果的影响可忽略不计。而反应中还原剂是过量的,假定还原反应进行得非常彻底,那么还原剂浓度、体积、水浴温度及保温时间的微小变化所产生的不确定度也可忽略不计。实际上,由于还原剂是现配现用的,水浴温度、恒温时间并非一个精确值,而是一个控制范围,这些因素在控制范围内的变化是随机的,因而对不确定度的影响也是随机的。因此,还原裂解产生的不确定度即使存在,也应包括在A类不确定度中。

2. 4　分离浓缩产生的不确定度

由于洗提液是过量的,洗提液体积产生的不确定度可忽略不计,而硅藻土萃取、旋转蒸发浓缩、氮吹等操作带来的芳香胺损失是随机的,构成了A类不确定度的主要来源。

2. 5　定容测量产生的不确定度

2. 5. 1　样液定容产生的不确定度

主要为三个方面:移液管校准产生的不确定度、温度和重复性变化。

2. 5. 2　样液测量产生的不确定度

按GC-MSD内标法测得样液与内标的峰面积来计算样液体积。其不确定度主要来源有:GC-MSD校准产生的不确定度、进样体积产生的不确定度,以及整个测量过程中随机因素(如人员、样品、仪器操作等)产生的A类不确定度。由于GC-MSD配置的进样装置为自动进样器,样液与标液使用同一支微量进样针,进样体积产生的不确定度可忽略不计,或可包括在GC-MSD校准产生的不确定度中。

2. 6　内标配制产生的不确定度

试验方法中,标液配制、样液定容所用溶液全部为内标溶液,其不确定度来源主要为称量、定容、移液产生的不确定度,以及测量产生的不确定度。

2. 7　标样配制产生的不确定度

2. 7. 1　标准储备液配制产生的不确定度

标准储备液浓度为:

ρcs = (m×P) /Vcs (2)

式中:ρcs ———标准储备液浓度,μg/mL;

m ———称取标准品的质量,μg;

P ———标准品纯度, %;

Vcs ——标准储备液定容体积,mL。

由式(2)可以看出,标准储备液配制产生的不确定度主要来源于称量、样品纯度及定容体积。

2. 7. 2　标准工作液配制产生的不确定度

标准工作液浓度为:

ρc=(ρcs×Vcs′)/Vc (3)

式中: ρc ———标准工作液浓度,μg/mL;

ρcs ———标准储备液浓度,μg/mL;

Vcs ′—— 配制标准工作液时移取的标准储备液的体积,mL;

Vc ——— 标准工作液定容体积,mL。

显然,标准工作液配制产生的不确定度,主要来自于标准储备液浓度、移取标准储备液的体积和标准工作液定容体积。

2. 7. 3　标准工作液测量产生的不确定度

与2.5.2节样液测量产生不确定度的来源相同。

2. 8　因果图

从不确定度来源分析发现,每个不确定度因素中都有A类不确定因素,为使输入数据关系和范围更加明确,将这些A类不确定因素单独列出,在因果图中插入额外影响因子“重复性”,以简化对不确定度分量量化的计算,此时,公式(1)演变为:

W =	As×AISS×ρc×V	×F (4)
	Ac×AISC×mE

其中, F是重复性测试产生的不确定度。因果图如图1所示。

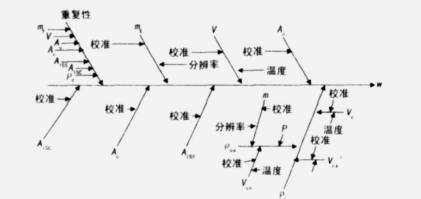
图1　测量过程中不确定度来源的因果图

3　不确定度的量化、合成

3. 1　样品质量引入的不确定度

3. 1. 1　天平校准产生的不确定度

称量使用分辨率为0.01g的电子天平,校准证书给出的不确定度为0.01g, k=2。考虑天平称量分两次完成,一次是空盘,另一次是毛重,因此,天平校准产生的不确定度uc(m)=2×1 ×0.01/2=0.0071g。

3. 1. 2　天平分辨率产生的不确定度

所用天平为数显式,其分辨率为0.01g。由于分辨率较大,重复测试的不确定度可忽略。按平均分布,则:ur(m)=0.01/3 = 0.0058g

3. 1. 3　样品质量产生的不确定度

样品质量(m)的不确定度合成为:

u(m) = √[uc²(m)+u²r(m)] = 0.009 g,自由度为∞。(注：数学符号√[… ]，代表平方根中的算式，下同)

相对不确定度为: u(m)/m = 0.009

3. 2　样液定容产生的不确定度

3. 2. 1　移液管校准产生的不确定度

样液使用2mL的移液管定容,经校准符合A级,允差为±0.012mL,假定均匀分布,则移液管校准产生的不确定度为:

uc(V)=0.012/3=0.0069mL

3. 2. 2　移液温度产生的不确定度

移液管的校准温度为20℃, 实验室的温度为(20±5)℃,温度变化为平均分布。甲醇的膨胀系数为1.19×10^-3/℃,远大于玻璃容器容积的膨胀系数,因此可忽略温度对容器容积的影响。假定满足矩形分布,则温度对体积的测量影响为:

ut(V)=5×1.19×10^-3×2/3= 0.0069mL

3. 2. 3　样液定容体积产生的不确定度

样液定容产生的不确定度为:

u(V)=√[u²c(V)+u²t(V)]=0.010mL,自由度为∞。

相对不确定度为: u(V)/V=0.010/2=0.005

3. 3　样液测量产生的不确定度

由于A类不确定度因素以重复性因素的形式单独列出,所以此处只需考虑校准产生的不确定度。根据校准证书, GC2MSD测量不确定度为5%,k=2。样液的测量同时包括对样液中内标的测量,因此,

u(As)=5%×14704230.63/2=367605.8

u(Aiss)=5%×3055317.75/2=76382.94

ν(As)=ν(Aiss)=∞

相对不确定度为: u(As)/As=u(Aiss)/Aiss=0.025

3. 4　标准储备液配制产生的不确定度

3. 4. 1　标品纯度产生的不确定度

根据标准品证书,4,4′-二氨基二苯甲烷纯度为:97.8% ±1%,置信水平为95%, n=6,按υ= 5查t分布表得,包含因子k = 2.57,则:

u(P)=1%/2.57=0.39%

3. 4. 2　标品称量产生的不确定度

标准品称量使用分辨率为0.0001g的电子天平,根据校准证书,该天平不确定度为0.3mg, k =2,配制浓度为1000mg/kg的标准储备液需称取0.0256g标品,因此:

uc(m)=2×0.0256×0.0003/2=0.000005 g

ur(m)=0.0001/3=0.000058g

合成的不确定度为

u(m) =√[uc²(m)+ur²(m)] =0.00006g,自由度为∞。

3. 4. 3　储备液定容产生的不确定度

储备液使用25 mL的A级单标线容量瓶定容,校准证书给出的允差为±0. 03 mL,校准温度为20 ℃,由3. 2节可知,

uc(Vcs)=0.03/√3 =0.0173mL;

ut(Vcs)=5×1.19×10^-3×25/√3 = 0.0859 mL

u(Vcs)=uc²(Vst)+ut²(Vst)=0.088mL,自由度为∞。

3. 4. 4　储备液浓度的不确定度

根据公式ρcs=m×P/Vcs可得:

ρcs=0.0256×106×7.8%/25=1001.47(μg/mL)

u(ρcs)=ρcs×√[	u(m)	]^2+[	u(P)	]^2+[	u(Vcs)	]^2= 5.82(μg/mL)
	m		P		Vcs

由于u(m)、u(P)、u(Vcs)自由度均为∞,因此,ν(ρcs)=∞

3. 5　标准工作液配制产生的不确定度

3. 5. 1　移液体积产生的不确定度

配制30 mg/kg标准工作液移取的储备液体积为0. 3 mL,使用经校准符合A级的1 mL分度吸管,容量允差为±0. 008 mL,由3. 2节可知,

uc(Vcs′) = 0.008/3 = 0.0046mL

ut(Vcs′) = 5×1.19×10^-3×0.3/3 = 0.0010mL

u(Vcs′) =√[uc²(Vst′)+ut²(Vst′)]= 0.005 mL,自由度为∞

3. 5. 2　标准工作液定容产生的不确定度

标准工作液用A级10 mL的容量瓶定容,校准证书给出的允差为±0. 02 mL,由3. 2节可知,

uc(Vcs) = 0.02/√3 = 0.0115(mL)

ut(Vcs) = 5×1.19×10^-3×10/√3 = 0.0344(mL)

u(Vcs) =√[uc²(Vcs)+ut²(Vcs)] = 0.036mL,自由度为∞。

3. 5. 3　标准工作液浓度的不确定度

根据公式ρc =ρcs ×Vcs ′/Vc

ρc=1001.47×0.3/10 = 30.04μg/mL

u(ρc)=ρc√[	u(ρcs )	]^2+[	u(Vcs′)	]^2+[	u(Vc)	]^2
	ρcs		Vcs′		Vc

=30.04×√[（	5.82	)^2+(	0.005	)^2 +(	0. 036	)^2]= 0.54μg/mL
	10001.47		0.3		10

由于u(ρcs)、u(Vcs′)和u(Vc)的自由度均为∞,因此,ν(ρc)=∞

相对不确定度为: u (ρc ) /ρc = 0. 54 /30. 04 = 0. 018

3. 6　标准工作液测量产生的不确定度

因所有测量使用的是同一台仪器,故与样液测量一样,用于校正的标准工作液测量时产生的不确定度:

u(Ac) = 5%×5695806.875/2 = 142395.2

u(Aisc) = 5%×3009231.75/2 = 75230.79

ν(Ac) =ν(Aisc) = ∞

相对不确定度为: u(Ac)/Ac = u(Aisc)/Aisc = 0.025

3. 7　重复性测量产生的不确定度

同一样品由不同人员在不同时间测量的数据如表1所示。

表1　重复测量数据

序号	1	2	3	4	5	6	7	8	平均值
含量	148.80	154.06	172.16	145.64	160.68	145.02	168.98	183.36	159.8

ua(F) = √	Σi=1	(Xi -X )^2	= 13.97mg/kg,ν(F) = 7
	8-1

相对不确定度为:

ua(F /F = 13.97/159.8 = 0.087

2. 8　合成不确定度

[	uc(w)	]^2=[	u(As)	]^2+[	u(Aiss)	]^2+ [	u(ρc)	]^2+ [	u(V)	]^2
	w		As		Aiss		ρc		V

+[	u(Ac)	]^2+[	u(Aisc)	]^2+[	u(m)	]^2+[	u(F)	]^2
	Ac		Aisc		m		F

uc(w) = 159.8×√[0.0252+0.0252+0.0182+0.0052+0.0252+0.0252+0.0092+0.0872] = 16.4mg/kg

3. 9　扩展不确定度与有效自由度

按照国际惯例,取扩展因子k=2,则扩展不确定度为: U = kuc(w) = 28.8mg/kg,有效自由度为:

υeff=	(uc(w)/w)^4
	(u(As)/As)^4	+	(u(Aiss)/Aiss)^4	+	(u(ρc)/ρc)^4	+	(u(V)/V)^4	+
	υA s		υA iss		υρc		υV

（(uc(w)/w)^4）							=13.3
(u(Ac)/Ac)^4	+	(u(Aisc)/Aisc)^4	+	(u(m)/m)^4	+	(u(F)/F)^4
υA c		υA isc		υm		υF

4　结论

经过测试,样品的4, 4′2 二氨基二苯甲烷含量为(159. 8 ±16. 4) mg/kg, k = 2,有效自由度υeff = 13. 3。比较各分量的相对不确定度可知,合成不确定度的来源中,重复测量产生的不确定度对不确定度总量贡献最大,即在测量中由过程随机效应导致的不确定度是造成结果偏差的主要因素, 这可能是由于EN14362 - 2: 2003规定的检测过程(保险粉还原、硅藻土吸附、液液分配、蒸发浓缩,氮吹)繁琐,造成芳香胺损失较大,也可能是因为芳香胺性质不稳定,易挥发而造成的。

参考文献:

[1] ISO/IEC17025 1999,测试和校准实验室能力的通用要求[S].

[2] EN14362-2:2003,纺织品——某些从偶氮染料分解得到的芳香胺的检测方法,第2部分:萃取法[S].