石墨烯在电化学储能过程中理论研究进展yd20219
苏方远,谢莉婧,孙国华,孔庆强,李晓明,刘卓,陈成猛 中国科学院山西煤炭化学研究所 炭材料重点实验室, 山西 太原030001
收稿日期:2016-04-26;
修回日期:2016-07-30
基金项目:国家自然科学基金(51402325).
通讯作者:陈成猛,副研究员. E-mail: ccm@sxicc.ac.cn
作者简介:苏方远,博士,助理研究员. E-mail: sufangyuan@sxicc.ac.cn
原载:新型碳材料2016
【摘要】本文对目前石墨烯在电化学储能过程中理论计算的研究进行系统整理,从石墨烯材料电子结构特征出发,对其在超级电容器、锂离子电池和氧还原过程中石墨烯起的作用进行综述,详细讨论了石墨烯在以上不同电化学环境中与物质的相互作用机制,为新型石墨烯基电化学储能器件的研究提供理论基础和研究思路。
【关键词】石墨烯; 电化学储能; 理论计算; 电子结构
【中图分类号】TQ127.1+1 文章编号:1007-8827(2016)04-0363-15 文献标识码:A
1 前言
石墨烯由于具有二维平面几何特征和独特的电子行为被广泛用于电化学储能研究领域,改善诸如超级电容器、锂离子电池的输出性能和提高氧还原过程(ORR)电催化活性。目前文献中大量实验结果报道也证实了石墨烯对不同储能领域场合的作用[1-7]。同时,研究者们也进行了大量的理论计算,从原子和电子的层次对石墨烯的作用机制进行解释。本文将对目前石墨烯在电化学过程中的理论计算结果进行综述,以超级电容器、锂离子电池和ORR过程为典型代表,整理目前得到的重要结论,加深对石墨烯功能的理解,也为新型石墨烯基电化学储能器件提供研究思路。
从电化学角度来讲,石墨烯在储能器件中所起的作用主要有四种:一种是石墨烯不参与电化学反应,仅仅通过与电解液形成双电层作用来存储电荷,提高电容效果,这种情况主要出现在超级电容器中;另一种则是与活性物质发生电化学反应,通过电子转移而产生法拉第电流,并为电化学反应的生成物提供存储场所,如锂离子电池等,或者虽然不发生电化学反应,但是可以通过与生成物相互作用而将其固定,同样提供存储场所,如锂硫电池[8];同时,石墨烯还可以为电化学反应提供催化效果,降低电化学反应所需的能量势垒,如ORR等;还有一种则是利用自身导电性提高电极的电导率,降低充放电过程中的欧姆电阻。最后一种跟具体电极制备过程密切相关,所以目前的理论计算主要集中在前三个方面,本文也将主要围绕前面三种作用展开。
非法拉第过程中,石墨烯吸附电解液中的离子,根据离子类型、电解液浓度不同,离子在石墨烯表面形成不同的排列方式,同时内部的电子也会聚集在石墨烯边缘与电解液中离子形成电荷相反的聚集层,从而形成双电层结构。石墨烯内部的电子会因为充电或放电过程占据不同的能级。其中,石墨烯的电子聚集引起的电容往往称为量子电容CQ。电容器的总电容CTotal与电解液中离子层电容CIon和石墨烯的量子电容CQ具有倒数和的关系:
|
|
根据电容的定义,量子电容![]() ,Q是在充电或者放电时石墨烯电极上的由于电子引入或释放而产生的额外电量,φ是石墨烯上的外电势。当石墨烯外电势为增加φ时,电子的电化学势变化为eφ,此时石墨烯所带的额外电荷为[9]:
,Q是在充电或者放电时石墨烯电极上的由于电子引入或释放而产生的额外电量,φ是石墨烯上的外电势。当石墨烯外电势为增加φ时,电子的电化学势变化为eφ,此时石墨烯所带的额外电荷为[9]:
|
|
其中,E是相对于费米能级的能量,f(E)是费米-狄拉克分布函数。
所以量子电容的差分电容可以通过以下得到:
|
|
可以看到,石墨烯的量子电容与其电子态密度DOS直接相关,通过使用DFT计算得到DOS,就可以通过以上公式计算量子电容CQ。
金属中的电子在费米能级处的电子态通常非常高,所以量子电容不是金属电极总电容的影响因素。而完整石墨烯由于费米能级处电子态密度非常低,量子电容CQ往往是限制总电容的主要因素[10, 11]。
石墨烯跟电解液反应物发生电荷转移的法拉第过程中,转移的速率的大小直接决定着电化学反应的快慢程度。根据Gerischer-Marcus理论[12-15],在石墨烯与电解液的反应过程中,电子转移速率kET如下:
|
|
|
|
εox为几率函数,DOSgraphene(E)的为石墨烯的态密度,Wox(λ,E)为电解液中电子态的分布,λ为重组能。可以看出,决定电化学反应过程的重要因素是石墨烯电子的态密度DOS与电解液中离子电子态的能量重叠程度。如果二者重叠程度较高,则电化学反应仅需要很小的过电位就可发生,而如果二者重叠程度较低,为了发生电化学反应则需要在较大程度上调整过电位,将二者重叠程度增大到一定程度。该理论同样也适用于石墨烯的电催化过程。
通过以上分析可以看出,石墨烯在储能体系中的电化学行为与其电子结构息息相关。正确认识其电子结构将是更好利用石墨烯材料的有效前提,并且也可以为具体应用领域中石墨烯材料的电子结构调整提供指导思路。
2 石墨烯电子结构特征
2.1 石墨烯及其缺陷类型
石墨烯属于由双原子基点组成的三角布拉维点阵。由于相邻的两个碳原子位置不等同,石墨烯晶格可以分为两个亚点阵,每个亚点阵都是三角布拉维格子。相邻两个C原子的间距为0.142 nm,键角为120°,与分子苯中的数值相同。平面内部C原子通过三个σ键相互相连,在垂直平面上碳原子的pz轨道形成离域的π键。
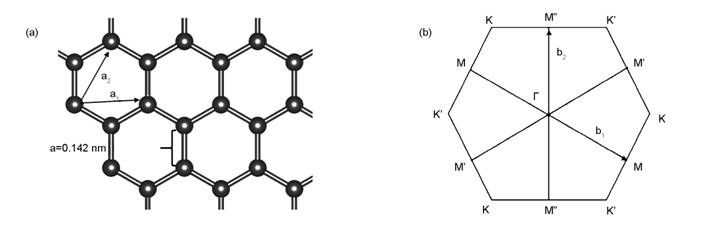
图1给出了石墨烯的结构示意图。如图1a所示,石墨烯单胞中两个C原子位于a1和a2为基矢的六边形的顶点,点阵的基矢如下:
|
|
点阵常数 a=|a1|=|a2|=2.46 Å。
石墨烯的倒易点阵的基矢b1 、b2 可以通过将实空间的基矢 a1和a2 旋转30°得到。基矢b1 、b2 分别为
|
|
布里渊区的三个高对称点是Γ, K 和 M, 分别是六边形的中心、角和边的中心,见图1b。
石墨烯的能带结构非常特殊,在倒易空间的K/K’处出现线性色散,即此处附近石墨烯电子能量线性变化,同时此处电子态密度为零。完整石墨烯的费米能级与Dirac点重合,在费米能级附近成键的π态和反键的π*态双重简并。
在石墨烯实际制备过程中,往往难以得到完整的石墨烯,总是存在各种缺陷。同时为了改善石墨烯的电子结构,赋予其不同的化学性能,研究者也会对石墨烯晶格进行调整,引入部分缺陷或异原子[16]。石墨烯上常见的缺陷为Stone-Wales(SW)缺陷、单空位(V1)缺陷、双空位(V2)缺陷和多原子缺陷[17, 18],同时还会存在一维线形缺陷和晶界引起的缺陷等。
|
|
|
图 1 石墨烯结构特征:(a)晶体结构, (b)布里渊区 |
存在SW缺陷的石墨烯并没有丢失C原子,只是将某个C—C键旋转了90°,相邻的四个六边形变成两个五边形和两个七边形,所以此类缺陷也常称为55-77缺陷。该缺陷的形成能非常高,缺陷位置相对固定[19]。存在SW缺陷时,石墨烯的费米能级与Dirac点仍然重合,但由于C—C键的旋转,Dirac点处π*带不再简并,在略高于费米能级处出现了一条由缺陷周围C原子的pz态组成近乎水平的能带[20]。
当石墨烯失去一个C原子后,会出现一个空位,产生V1缺陷。由于C原子的缺失,石墨烯上会出现三个具有未饱和悬挂键的C原子,此时石墨烯发生Jahn-Teller形变,其中两个C原子相互靠近形成五边形,只留下一个悬挂键。从而出现一个5元环和一个9元环。该缺陷的形成能也非常高,但是其迁移能垒较低,在较低温度下就可以在石墨烯表面发生迁移[21]。由于V1缺陷的存在,石墨烯的费米能级相对于Dirac点降低,并且费米能级附近π和π*的简并度也被破坏,二者不再重合。在费米能级附近出现由没有连接的C原子上未饱和σ态形成的缺陷能带和由与缺失的C原子不在同一亚点阵的C原子上pz形成的π缺陷态。
当两个相邻的碳原子除去后,石墨烯上会出现V2缺陷。此时石墨烯上的4个6元环会变成两个5元环和一个8元环,即585-V2。该缺陷的形成能与单空位相当。V2缺陷电子结构与石墨烯相比发生了很大的变化,费米能级与Dirac点不再重合,在高于费米能级处出现了由缺陷周围C原子的pz态形成的几乎水平的能带[22]。同时,在费米能级上面还存在由结构弛豫后连接到一起的两个C原子σ态形成的能带。V2缺陷并非一种,当8元环中的一个C—C键旋转90°后,会变成555-777的V2缺陷,该缺陷的形成能比585-V2低[23, 24]。如果进一步旋转555-777-V2缺陷上另外一个C—C键,会形成555-6-777-V2缺陷,其形成能介于585-V2和555-777-V2之间。V2缺陷的迁移能远高于V1,所以除非在高温下,V2在石墨烯表面上基本上是固定的[25]。
当更多原子被除去后,会产生更加复杂的点缺陷。计算表明,当失去偶数碳原子后,由于会形成饱和的结构,形成能略低,但是失去奇数碳原子后,会出现不饱和键,形成能会高于前者,并且化学反应性也较高[26]。
除了点缺陷之外,石墨烯内部还存在一维的线缺陷。一种是将不同取向的石墨烯微晶分开的晶界,通常由5元环、8元环组成[27]。还有一种则是石墨烯的边缘。由于具有悬挂键,边缘结构式通常为armchair和zigzga取向。然而当这两种边缘有碳原子丢失时,边缘的六元环中间会产生五元环和七元环[28]。
2.2 原子掺杂
N原子经常引入到石墨烯内部来调控其电子结构。N掺杂石墨烯可以通过含N前驱体对石墨烯或者氧化石墨烯后处理得到[29, 30]。研究者通过多种实验表征手段证明N在石墨烯晶格内部主要是以石墨化N、吡啶N和吡咯N的形式存在[31-34]。吡啶N和吡咯N主要位于石墨烯的边缘和缺陷位,石墨化N则是与石墨烯内部三个C原子相连,不产生空位缺陷。由于N的原子尺寸小于C原子,石墨化N的N—C键长为1.41 Å,略低于C—C键的1.42 Å。对于石墨化N掺杂的石墨烯,由于N上富余电子进入π*,费米能级向上移动进入导带。此时费米能级附近π和π*的简并度在一定程度上被破坏。同时在略高于费米能级处出现了杂化电子态,并且与其中一条π*带杂化[22, 35]。
缺陷点的存在会减少N掺杂的形成能,所以N在缺陷石墨烯的掺杂比完整石墨烯容易,在N掺杂之前有意引入缺陷会提高掺杂效果。同时,N掺杂之后缺陷的形成能也降低,表明N原子的存在也会有利于缺陷的产生。计算表明N倾向于掺杂在缺陷上具有较大收缩性键的C位置和五边形的顶点位置,前者是由于C—N键比C—C键短,后者是因为N进入五边形形成的吡咯结构具有更为稳定的芳香性结构。掺杂的N原子和石墨烯的点缺陷存在吸引作用,在各种缺陷中,V1缺陷与N的相互作用最强[36, 37]。对于完整石墨烯,由于N原子之间存在排斥力,N原子掺杂位置分布比较分散,但是当存在缺陷时,由于缺陷与N之间的吸引力,缺陷附近区域N的分布将会非常集中[36, 38]。
B原子也经常引入石墨烯来调整其电子结构。由于B比C缺少一个电子,掺B之后石墨烯费米能
级向低能级方向移动,与Dirac点不再重合[39]。此外,S、P等原子也用来掺杂改进石墨烯的电子结构[40, 41]。
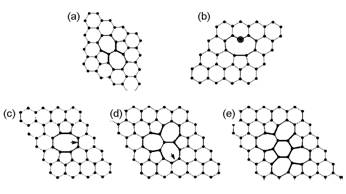
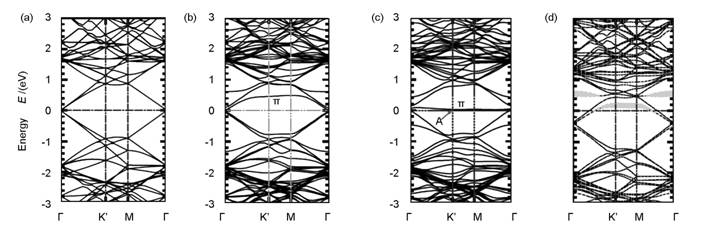
图2给出了SW缺陷、V1和V2缺陷的具体结构[17]。图3为完整石墨烯、585-V2石墨烯、SW缺陷石墨烯和石墨化N石墨烯的电子能带图[22]。
下面根据石墨烯在储能器件中所起的不同作用,分别从超级电容器、锂离子电池和ORR过程对目前的理论研究进展进行讨论。
|
|
|
图 2 不同种类石墨烯缺陷[17]: (a)S-W缺陷; (b)V1缺陷; (c)585-V2缺陷; (d) 555777-V2缺陷; (e) 555-6-777-V2缺陷 |
|
|
|
图 3 不同类型石墨烯能带结构[22]: (a)完整石墨烯; (b)585-V2缺陷; (c)S-W缺陷; (d)N石墨烯 |
3 超级电容器
Paek等计算了300 K时完整石墨烯的量子电容,发现量子电容随电势呈现U形变化,电势为0 V时量子电容具有非零最低值,并且在最低值两侧呈对称变化,这与实验测量得到的量子电容形状类似[42]。这表明,完整的石墨烯量子电容非常小,在充电或放电过程中难以为电子提供足够的能态来存储电荷。为了提高石墨烯的量子电容,首先考虑到的是在石墨烯中引入缺陷结构,改善石墨烯在费米能级处的DOS。Pak等对不同点缺陷结构石墨烯的电荷存储性能和量子电容进行了计算,发现不同缺陷都在很大程度上增加了石墨烯的电荷存储能力,进而提高了量子电容[43]。对于SW缺陷,由于费米能级处存在五元环和八元环碳原子上pz态组成的能带,该能带将会容纳额外的电子,进而提高石墨烯可聚集的电量。同时,由于存在pz准局域态,V2缺陷中缺陷附近的C原子也会容纳额外的电子。SW缺陷在作为负极时存储电荷非常有效,而V2缺陷则在作为正极时表现出良好的电荷存储行为。
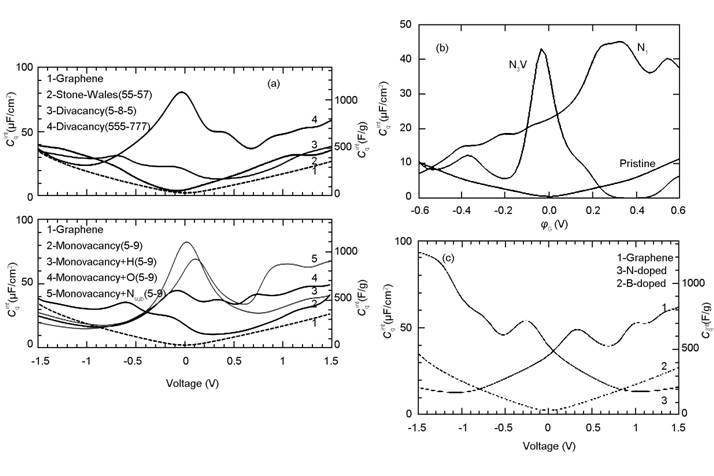
Paek等还就N原子对量子电容的的影响进行了计算[35]。N原子的引入可以有效提高费米能级附近的DOS,石墨化N和三吡啶N缺陷在φ=0 V时的量子电容最低值分别为22 μF/cm2和44 μF/cm2,远高于完整石墨的0.45 μF/cm2。在石墨化N中,量子电容随着φ增加而增加,在0.3 V时达到最大值45 μF/cm2,当φ低于0 V时,量子电容减小,在-0.85 V时趋向于零。对于三吡啶缺陷,当φ低于-0.2 V时,量子电容迅速降低到5-10 μF/cm2。Yang等研究了N掺杂和缺陷浓度对石墨烯电子结构和量子电容的影响[44]。对于V1缺陷,当浓度从1.4%增加到12.5%时,最大量子电容从54.51 μF/cm2增加到了124 μF/cm2。对于吡啶N掺杂,随着N原子浓度增加,自旋极化效应变强,当浓度从1.4%增加到12.5%时,最大量子电容从32.68 μF/cm2增加到了113.1 μF/cm2。Wood等也计算了缺陷和原子掺杂对石墨烯量子电容的影响,发现电容提高程度因缺陷类型和电压范围不同[45]。V2的555-777和存在H或者N的V1缺陷提高了费米能级附近的DOS,具有类似赝电容的特征,三者量子电容与电压的关系非常类似。这是由于三者类似的电子结构所导致,三种情况中均在费米能级附近都有新的来自缺陷周围C原子pz轨道所组成的半占据准局域态。吸附O的V1缺陷石墨烯的电容与电压关系与也与5-8-5的V2缺陷非常类似,但量子电容低于吸附H和N的V1缺陷。晶格中C原子被N和B替换后都会对量子电容产生影响,前者对正偏压范围内量子电容提高,后者则是对负偏压范围内量子电容提高。
同时,Wood等还详细讨论了石墨烯的层数、应力和表面褶皱等局部结构对量子电容的影响[45]。由于单层石墨烯带密度较低,难以有效屏蔽电极中产生的额外电荷,所以电压容易随电荷增加而迅速提高,电容效果较差。当石墨烯层数提高后,所能容纳的电荷数提高,量子电容相应提高。作者计算了ABA排列不同层数石墨烯对电极屏蔽性能的影响,发现薄的片层极化效应在电极中没有完全衰减,从六层石墨烯之后,屏蔽行为极大改善。对于更厚的片层,极化衰减行为可以用指数曲线来拟合。为了得到95%的的屏蔽效果,需要6.6 Å的厚度,这表明在电解液环境中至少需要六层或以上的石墨烯才能得到良好的屏蔽效果[46]。石墨烯受到张力后量子电容也会提高,提高的程度与张力方向无关,只跟张力的增加幅度有关。这是由于张力作用下,π/π*能带向费米能级附近移动,从而提高此处的DOS,进而改善了量子电容。石墨烯表面的局部曲度会将石墨烯中C原子的px/py态混合进pz态中,从而减弱π键,减小了π-π*的能级差,并增加了面内σ键的强度。π-π*能级差的减小可以在费米能级处产生更多的量子态,从而可以提高石墨烯的量子电容。曲度越大,以上的杂化作用就越明显,电容提升效果就越明显。Wood同时也考察了石墨烯中的周期性的折迭结构对量子电容的影响。与局部曲度不同,在折迭中心由于两边石墨烯片层靠的非常近,出现了类似石墨的区域,同时在边缘区域存在局部曲度。该结构在实验上也被证实是存在的[47]。由于费米能级上面π*带为量子电容的提高提供主要贡献,所以该结构下量子电容随电压变化不对称,在负偏压下电容改善效果明显。
图4为完整石墨烯、SW石墨烯、V1石墨烯、V2石墨烯、掺N石墨烯和掺B石墨烯量子电容的比较[35, 45]。当石墨烯在平面某个方向上尺度有限时会形成纳米带,此时电子结构特征与量子电容与完整石墨烯相比具有较大的变化。Pak等研究了具有zigzag边缘不同宽度的石墨烯纳米带边缘态对量子电容的影响[48]。计算表明边缘态的存在对量子电容的提高具有重要作用。边缘处准局域pz态在费米能级附近出现峰值,从而提高了量子电容。使用H将边缘态裸露的C原子钝化后,可以去除边缘碳上未饱和的sp2键而不影响π轨道。此时,随纳米带宽度增加,边缘的pz态与体系的π态相互作用增强。而当使用—OH钝化边缘时,窄的纳米带上pz态的峰值变宽,表明可能与O的2p轨道有作用,但是在宽纳米带上却没有变化,说明此时边缘pz态与π体系相互作用较强,不再跟O的2p有明显的作用。宽度较窄时,—OH钝化的纳米带量子电容明显高于H钝化纳米带的值,但是当宽度较宽时则二者电容的差别不再明显。同时,与完整石墨烯不同,zigzag边缘的石墨烯纳米带电极的量子电容曲线在阴极和阳极形状不同,不再对称。
过渡金属原子也会对石墨烯的电子结构产生影响,并在石墨烯的空位上产生较强的吸附作用[49, 50]。Paek等研究了过渡金属-石墨烯上V1缺陷和V2缺陷相互作用对电子结构和量子电容的影响[51]。引入过渡金属后形成金属-空位相互作用,空位附近碳原子的sp2和pz轨道与过渡金属的d轨道作用产生准局域的电子态。由于引入了更多的电子态,量子电容有了不同程度的提高。
|
|
|
图 4 不同结构石墨烯量子电容[35,45]: (a) 缺陷石墨烯, (b) N掺杂石墨烯, (c) N、 B掺杂石墨烯 |
4 锂离子电池
虽然石墨烯用于锂电负极目前不太容易实现,但由于石墨烯良好的导电效果可以作为活性材料的导电剂用于锂离子电池,提高其倍率性能和循环性能,所以研究Li与石墨烯的相互作用仍有重要的理论意义[52, 53]。锂离子电池的石墨烯理论研究主要集中在两个方面,首先是容量问题,涉及到Li与石墨烯的相互作用,再就是Li离子在石墨烯上的扩散问题,这与锂离子电池的倍率性能紧密相连,主要包括Li在石墨烯表面平行方向的扩散和穿过石墨烯表面的扩散。
4.1 容量与相互作用能
4.1.1 完整石墨烯
Li在完整石墨烯表面的相互作用研究表明,Li稳定存在于石墨烯的C六元环中间,组成环的六个碳原子都与Li产生相互作用,而Li在两个碳原子的桥接位置和单个碳原子的顶端位置时的相互作用非常弱[54]。Li与C六元环的相互作用具有离子键特征,电荷从Li向石墨烯转移[55],迁移的电子主要集中在Li和C六元环之间的区域,所以Li原子上面区域和石墨烯上C-C键上的电子减少。当Li吸附在石墨烯表面时,石墨烯的电子结构有了一定的变化。由于Li的电子进入石墨烯的π*带,体系费米能级明显上移,进入导带,同时Li的2s态由于电荷转移位于高于费米能级的位置,此时石墨烯仍然有Dirac点,但是由于电荷从Li转移到了石墨烯,费米能级变得略高于狄拉克点[56, 57]。
通常采用Li在石墨烯表面的吸附能![]() 来描述Li与石墨烯作用过程。
来描述Li与石墨烯作用过程。![]() 是Li与石墨烯系统的总能量,ELi是Li原子的能量,
是Li与石墨烯系统的总能量,ELi是Li原子的能量,![]() 是石墨烯没有Li时的能量。当计算
是石墨烯没有Li时的能量。当计算![]() 时,ELi的数值取决于Li参考状态的选取,从而Li的参考状态直接决定了
时,ELi的数值取决于Li参考状态的选取,从而Li的参考状态直接决定了![]() 的大小。早期研究中,通常采用气相中孤立Li原子为参考态得到的ELi来计算吸附能,此时
的大小。早期研究中,通常采用气相中孤立Li原子为参考态得到的ELi来计算吸附能,此时![]() 为负值,表明Li在石墨烯表面发生吸附时释放热量,该过程可以自发进行。从而很多结果都指出石墨烯是一种理想的锂离子电池负极材料,并且两侧都可以对Li进行吸附,甚至提出了Li2C2结构[54, 57-69]。
为负值,表明Li在石墨烯表面发生吸附时释放热量,该过程可以自发进行。从而很多结果都指出石墨烯是一种理想的锂离子电池负极材料,并且两侧都可以对Li进行吸附,甚至提出了Li2C2结构[54, 57-69]。
Lee等使用Li金属作为参考态系统研究了不同含量Li在石墨烯上的状态,与气相中Li原子相比,Li金属作为参考态更加符合实际情况。计算结果表明,此时Li与石墨烯的吸附能大于0,表明Li与完整石墨烯不会自动发生吸附作用,难以形成稳定化合物[70]。而对于少层石墨烯,Li则会与之自动发生反应。当Li进入少层石墨烯的层间时,Li与碳原子的相互作用受层间范德华力的影响,并且该影响随着Li含量变化而变化。计算结果表明,少层石墨烯存储Li的容量低于本体石墨。Li可以进入任何层数的少层石墨烯中,但是只能进入石墨烯层间,不能存在于少层石墨烯的表面。对于两层石墨烯,当含量低时Li具有非常强的插层作用。当石墨烯层数继续增加时,Li首先进入最外面的石墨烯层间,而不是中间的层间。随后Li根据石墨烯层数的不同而具有不同的嵌入行为,或进入同样的最外层间,或进入另一个最外层间或者进入内部层间。
Fan等采用Li在本体Li金属的状态作为参考态,考察了Li在石墨烯上的吸附行为[71]。采用该参考态时,Li在石墨烯表面的吸附能为负值,说明可以发生吸附,但是容量仍然低于石墨。石墨烯上不同Li原子之间存在库伦排斥力,当Li的浓度很低时Li倾向于在石墨烯表面分散,故当浓度非常低时Li可以吸附在石墨烯上。但随着Li增多,Li原子之间由于相互吸引会形成团簇而与石墨烯发生相分离,所以石墨烯的容量比石墨低。作者分析了Li团簇在石墨烯的吸附,发现吸附到石墨烯上团簇的内聚能高于孤立团簇的内聚能,表明前者更为稳定。团聚进一步发展则会形成枝晶。Liu等的计算也表明,由于Li-石墨烯体系的不稳定性和Li-Li之间的排斥,随着Li的增加,Li-石墨烯体系的能量升高,并且由于Li-石墨烯的能量高于Li的内聚能,Li在石墨烯表面倾向于发生相分离而形成Li枝晶[72]。
4.1.2 缺陷及杂化石墨烯
Li与带有缺陷的石墨烯的相互作用与完整石墨烯具有较大的差异[56]。Li与585的V2缺陷石墨烯作用时,由于Li电子的转移,V2石墨烯上费米能级附近原来近乎水平的能带由于部分被电子占据而能量降低。然而,费米能级仍然在Dirac点下方。Li与SW缺陷的石墨烯作用时,费米能级升高超过Dirac点而进入导带,同时SW缺陷出现的那条近乎水平的能带也部分被占据。
SW缺陷石墨烯上电荷转移的区域与完整石墨烯类似,然而对于V2缺陷的石墨烯,Li下方聚集的电荷明显减少,从而降低了Li扩散通过时的阻碍。当存在V1缺陷时时,具有悬挂键C原子的2s、px和py态与Li的2s轨道在费米能级处发生重迭,表明这两个原子发生了键合作用。电子在此区域富集。所以,Li与V1缺陷石墨烯相互作用更强,导致了DOS峰的变宽和移动[57]。
对于完整石墨烯,Li与石墨烯表面的距离是1.72 Å,Li-C键长是2.24 Å。当Li与缺陷石墨烯作用时,最稳定的Li结合点同样是在空位。对于SW缺陷,Li与石墨烯平面距离是1.59 Å, V2缺陷中该值是1.43 Å。从距离可以看出,Li与带有V2缺陷的石墨烯相互作用最强。当V2密度最高时(25%),石墨烯可以容纳的最高容量为1 675 mAh/g,锂化电势约为0.1 eV;对于SW缺陷,密度最高可以为100%,此时石墨烯全部由五元环和七元环组成,容量为1 100 mAh/g[73]。
Ma等研究了N掺杂石墨烯与Li的相互作用[74]。使用石墨化N、吡啶N和吡咯N作为研究对象。与完整石墨烯不同,由于N引入了富余的电子,Li在石墨化N的石墨烯表面的稳定位置为与N原子对角的C原子顶端,并且Li的吸附能也略低于完整石墨烯。吡啶和吡咯N则不同,由于二者都是缺电子态,Li的最稳定吸附位为与N原子直接相连,吸附能远高于完整石墨烯,并且吸引更多的电子。吡啶N的DOS在此处出现一个p轨道的尖峰,正好与Li的2p轨道位置一致,表明N原子和Li的轨道发生杂化作用。然而,石墨化N中N的电子态则有很大的区别,不与Li的P轨道作用。所以后者的束缚能低于前者。
当有更多Li进入石墨烯时,无N的缺陷石墨烯、吡啶石墨烯和吡咯石墨烯上Li都排列为两层,第一层的Li除了位于缺陷中心之外,距离石墨烯2.1 Å,第二层分别为4.0、4.2和3.8 Å,无N的缺陷石墨烯上第一层有8个Li,而后两种结构上有9个Li。第一层Li的位置都在石墨烯六元环中间的上方和缺陷中心。可以说,N掺杂后,石墨烯上吸附Li的位置增加了。Li2放在吡啶N石墨烯上的Li-Li变成了3.42 Å,吡咯上变成了3.08 Å,都高于原来的2.71 Å。同时Li2在上述两个表面的吸附能分别为1.26 eV和1.19 eV,均高于其束缚能1.02 eV,所以Li不太容易在掺N石墨烯表面形成枝晶团簇。
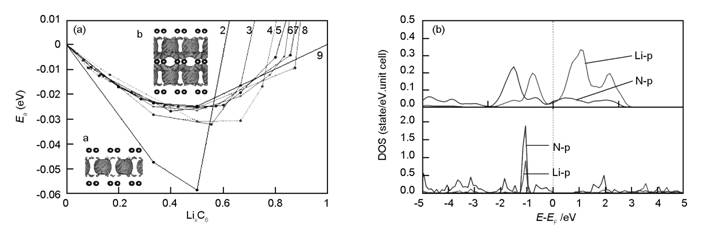
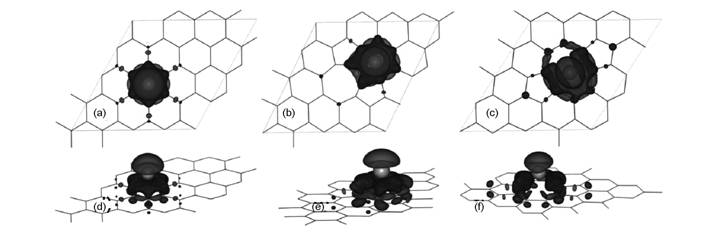
图5 为不同层数石墨烯[72]和掺N石墨烯[74]与Li相互作用,图6为Li在缺陷石墨烯上电子差分密度图[75]。
|
|
|
图 5 不同结构石墨烯与Li相互作用[72,74]: (a)少层石墨烯, (b) Li与掺N石墨烯的态密度 |
|
|
|
图 6 Li在缺陷石墨烯上电子差分密度图[75]: (a, d) 完整石墨烯, (b, e) V1 缺陷, (c,f) V2 缺陷 |
4.2 扩散
锂离子电池系统中,石墨烯除能够存储Li之外,还有一个重要的考察因素是石墨烯对Li离子扩散过程的影响,这直接影响锂离子电池的快速充放电行为。扩散过程包括两方面,Li在石墨烯表面上并以与表面平行的方向进行扩散,另外一种是穿过石墨烯平面,以与平面垂直的方向扩散。
计算表明,Li在完整石墨烯表面的扩散势垒是0.32 eV,表明Li易沿着石墨烯表面扩散[57],利用石墨烯作为负极时往往具有良好的倍率性能。Fan等的计算结果表明,当Li在完整石墨烯上沿着六元环中心顶部—C—C键中间-六元环中心顶部路径扩散时,最高的能量阻碍在Li跨过C—C键的位置,能量势垒为0.311 eV;沿着六元环中心顶部—C原子顶部-六元环中心顶部扩散时,C原子顶点为能量壁垒,0.337 eV。当Li在两层石墨烯的层间扩散时,同样具有较低的扩散能垒[76]。
石墨烯的缺陷对Li在平行石墨烯平面方向的扩散行为具有重要影响。Li在585结构的V2缺陷中扩散时,由于缺陷产生的能量陷阱,Li很容易被固定在缺陷区域[72]。该缺陷上的扩散阻碍为0.17 eV,而V1的扩散阻碍则是0.24 eV,都小于完整石墨烯(0.311 eV),所以该能量陷阱可以很大程度上减小Li的扩散势能,进一步改善Li在石墨烯表面的扩散行为[76]。
石墨烯内部经常出现晶界,尤其在通过CVD法制备的石墨烯中更是常见。晶界缺陷也会对石墨烯费米能级附近的电子态产生影响。Zhou等详细研究了晶界对Li在石墨烯上的吸附和扩散行为[77]。计算结果表明Li在石墨烯上最稳定的吸附位置在晶界上。(5,0)|(3,3)晶界含有三个5-7环,最稳定的点为五边形的顶位,其次是七边形,最不稳定为六边形。(2,1)|(2,1)含有一个5-7环,七边形的吸附位比五边形和六边形稳定。(2,0)|(2,0)有两个五边形和一个八边形,Li倾向于吸附在八边形位置,并且比前两种晶界更为稳定。以上缺陷结构对Li的吸附能力都优于完整石墨烯。Li原子在石墨烯在平行和垂直晶界的扩散行为结果表明,Li原子在晶界上的平行扩散能垒明显低于垂直晶界的扩散,说明Li原子很难横向穿过晶界而到另外一个微晶区域。
Li在石墨烯片层垂直方向的扩散行为也对锂离子电池的倍率性能产生重要的影响[66]。Li透过完整石墨烯扩散时,由于库伦排斥力,能量势垒非常高,为9.8 eV,所以Li难以通过六元环中心穿过完整石墨烯表面[76]。当存在空位缺陷时,扩散阻碍降低。Lee等结合实验和理论计算了Li在不同石墨烯上穿过时的能量势垒,分别为完整石墨烯为10.2 eV,SW缺陷位6.35 eV,V1为8.86 eV,V2-585为2.36 eV[78]。所以从V2缺陷开始,Li基本可以透过石墨烯片层发生扩散。
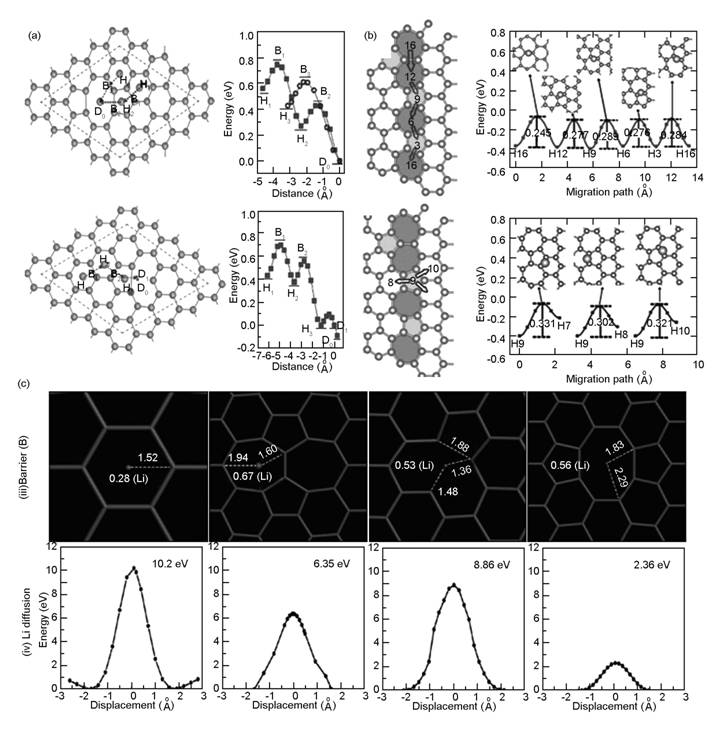
图7为Li离子在石墨烯上的扩散行为[76, 78, 79],其中图7a为平行石墨烯平面方向,图7b为平行石墨烯晶界方向,图7c为透过石墨烯平面方向。
|
|
|
图 7 Li离子扩散过程[76,77,78]: (a)平行石墨烯表面, (b)平行石墨烯晶界, (c) 透过石墨烯平面 |
5 ORR过程
燃料电池可以直接将化学能转变成电能,具有转化效率高,功率密度高和无污染的优点。O2还原反应是制约燃料电池发展的重要因素。该反应可以通过两种路径发生,第一是四电子过程,O2得到四个电子直接还原成H2O;第二是效率较低的两电子过程,O2转变为H2O2。由于利用效率高,四电子过程的催化剂研究非常重要。
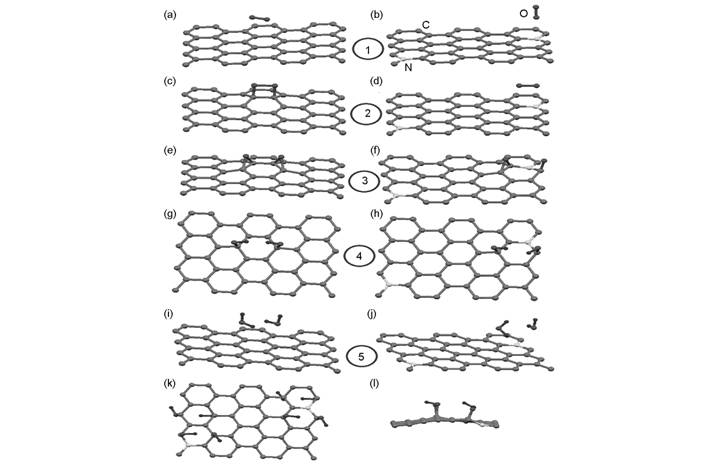
石墨烯催化效果计算表明, O2分子与完整石墨烯片层的吸附能都非常小,二者的距离也较大,大于2.6 Å[80]。虽然O2分子与石墨烯形成弱的离子键,但是由于反应过程中后续步骤所需能量非常高,并且生成的OOH也难以吸附在完整石墨烯上,所以完整的石墨烯没有O2催化活性[40, 81, 82]。由于N的电负性强于C, N周围的C原子带有正电荷,并且具有一定的自旋电荷。研究表明,当碳原子的自旋电荷密度或原子电荷密度高于0.15时就会具有ORR的电化学活性[41, 83]。Son等采用周期结构石墨烯模型详细探讨了完整石墨烯和掺N石墨烯上ORR过程,见图8,同时还计算了N石墨烯上N含量对ORR过程的影响,发现4%~5%的N含量对于应用是比较合适的[81]。
|
|
|
图 8 ORR在(左)完整石墨烯和(右)N石墨烯上的反应过程[81] |
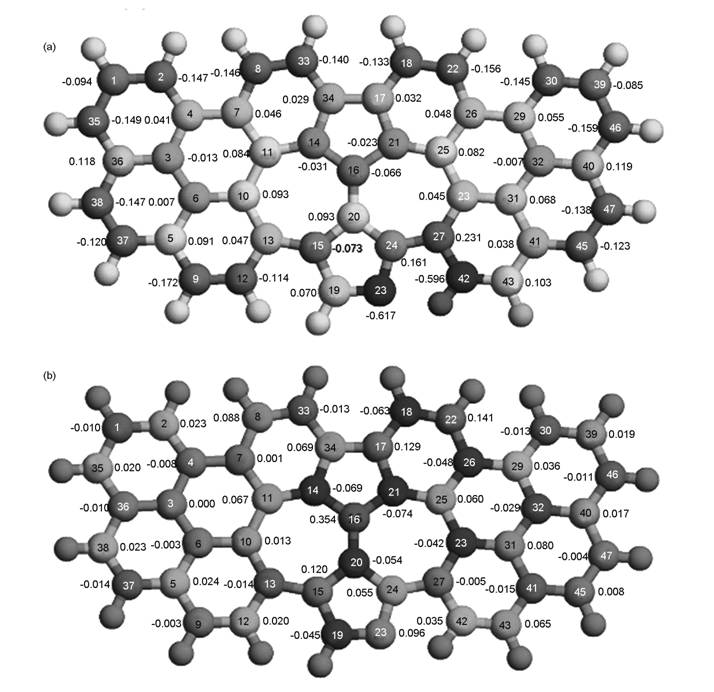
Xia等使用团簇结构的石墨烯模型研究了含N石墨烯在酸性环境中对O2的催化机理。计算表明,OOH吸附在靠近吡啶结构N的C原子上,其中一个O与C原子相互作用,并且该C原子从石墨烯平面伸出。对于吡咯N,OOH同样会吸附在靠近N的C原子上。当在OOH上进一步增加H后,吡啶N和吡咯N石墨烯上都会形成不稳定的HOOH,O—O键长增加,容易变成两个OH,所以在N石墨烯上的ORR是四电子过程。同时,作者提出自旋密度和电荷密度是决定催化效果的关键因素。尽管有的C电荷密度非常高,但是OOH更容易吸附在具有高自旋密度的C原子上。与电荷密度相比,自旋密度更能决定催化活性位,只有当自旋密度非常小时电荷密度才起作用[82, 83]。图9给出了所计算的掺N石墨烯上电荷密度和自旋密度分布[83]。
Cueto等使用团簇结构模型比较了S、P、N掺杂石墨烯在酸性环境中的ORR机理。发现P掺杂的石墨烯比N和S掺杂石墨烯作为催化剂更有优势[40]。对于N和B掺杂的石墨烯,OOH与C发生作用形成的O—C键的键长基本类似,但是低于P掺杂石墨烯,表明P石墨烯具有更好的催化效果。吸附能计算表明,B石墨烯的吸附能低于N和P石墨烯。对于N和P掺杂石墨烯,后者路径具有能量优势,吸附到N或P掺杂石墨烯上的OOH变成了两个OH。在后续步骤中,两个H持续加到两个OH上形成H2O,所以四电子还原过程优于两电子过程。与两电子过程相比,在酸性环境中,N和P石墨烯的四电子过程在能量上更有优势,同时P在反应上具有更高的效率。
|
|
|
图 9 N掺杂石墨烯的(a)原子电荷密度和(b)自旋密度[83] |
Jiao等[84]使用实验和理论计算研究了B、N、P、O和S掺杂的石墨烯在碱性环境中ORR的催化作用,发现电化学反应产物与OOH中间体在催化剂表面的束缚强度有关,同时束缚强度与每个ORR活性原子的分子价轨道能级相关。笔者使用活性中心最低价轨道能级与整个石墨烯最高价轨道的能级差来表征吸附的强度。良好的石墨烯基催化剂应该掺杂具有更高价带轨道能的ORR活性原子,从而带来更小的差值,提高中间体在表面的吸附。
如前面提出,N石墨烯的催化活性点是与N相邻的碳原子,这些C与完整石墨烯上相比具有更高的活性,但与O的亲和力与Pt金属相比仍很弱,催化活性有限。过渡金属具有更高的活性点,但是当Fe、Co、Ni和Cu等过渡金属原子吸附到完整石墨烯上时,由于与石墨烯之间较弱的吸附能,这些过渡金属容易发生团聚,并且会形成强度较高的O—M键,阻碍O原子的进一步反应而不太适合做为ORR的催化剂。但是当有V1缺陷或N原子掺杂时,金属原子可以紧密固定[85-87]在石墨烯表面,并且由于M与石墨烯C的作用,M—O键强度适中,可以吸附的O原子也可以脱除。由于M—O的键能能被调节到了合适的能级,过渡金属石墨烯催化效果与Pt类似,具有良好的ORR催化活性[88]。N掺杂石墨烯由于N可以与金属铆接也经常被用来作为贵金属催化剂的载体。理论计算[89]表明N可以调整石墨烯的电子结构,提高石墨烯与Pt原子的结合。
Wang等[80]研究了FeN4石墨烯上的ORR反应路径,发现OOH解离路径是能量最优的路径。O2分子在催化剂表面吸附后,会解离成两个O原子或者和一个H结合形成OOH分子。通过计算研究可以认为能量最优的路径是吸附的O2变成OOH,而不是变成两个O原子。所以,O2的分解路径不是动力学上的最优路径。OOH形成后,会通过断裂O—O键形成O和OH,或者进一步得到H形成HOOH,进而自发断裂其O—O键然后变成两个OH。计算发现在FeN4石墨烯表面,OOH的分解反应优于OOH继续加H。所以四个电子的OOH解离路径是ORR的最优路径。
Li-空气电池负极为Li,正极的空气电极通常为多孔炭,具有非常高的能量密度。外部的O2进入空气电极并吸附在多孔炭的表面,随后O2分解并与负极氧化得到的Li离子发生反应。Ouyang等[90]使用周期结构模型计算了Li-空气电池正极O2在N石墨烯表面的催化分解过程。O2分子靠近离石墨烯时,一个O原子位于N最邻近的C原子上面并向石墨烯平面倾斜,另外一个O位于C5N环的中心,O2不再平行,O—O键变弱。
除了在ORR反应中的催化作用,在O2析出反应中掺杂石墨烯也具有明显的电化学活性。理论计算表明,B掺杂的石墨烯由于缺电子,可以比完整石墨烯较强低吸附Li2O2,进而在较低能垒下活化Li—O键并将![]() 氧化成O2。由于B掺杂的石墨烯可以在很大程度上降低决速步骤的能垒,可以有效提高Li—空电池的电流密度[39]。
氧化成O2。由于B掺杂的石墨烯可以在很大程度上降低决速步骤的能垒,可以有效提高Li—空电池的电流密度[39]。
6 总结
综上可以看出,石墨烯在电化学储能过程中所起的作用与其电子结构紧密相关。完整单层石墨烯由于费米能级附近电子态有限,量子电容非常低,并且具有非常强的电化学惰性。除非用来降低电化学过程的欧姆电阻,完整单层石墨烯难以直接用于电化学储能领域。引入缺陷、杂原子、乃至过渡金属或增加层数都可以对石墨烯电子结构产生较大的影响,增加费米能级处的DOS。实验中实际制备得到的石墨烯并不是完整的单层石墨烯,往往带有一定的缺陷,并且层数也不全是单层。这些都将改善其量子电容,提高ORR电化学活性,为Li离子提供存储场所并为其扩散提供通道。这可能是目前在实验结果中石墨烯在电化学储能过程中表现出良好效果的主要原因。
DOS的提高在改善电化学活性的同时可能又会引入不可逆的副反应,影响器件的循环使用寿命。所以在对石墨烯进行改性时需要综合考虑可能发生的各种反应,使用理论计算对石墨烯的结构先行进行设计,综合考虑各种电化学反应的可能性,进而根据不同使用场合对其电子结构进行有目的地调整,将在很大程度上促进石墨烯基储能器件的深入研究。
参考文献:
[1] Li A H, Liu J Q, Feng S Y. Applications of graphene based materials in energy and environmental Sscience[J]. Science of Advanced Materials, 2014, 6(2): 209-234.
[2] Lu Y H, Huang Y, Zhang M J, et al. Nitrogen-doped graphene materials for supercapacitor applications[J]. Journal of Nanoscience and Nanotechnology, 2014, 14(2): 1134-1144.
[3] Wu S P, Xu R, Lu M J, et al. Graphene-containing nanomaterials for lithium-ion batteries[J]. Advanced Energy Materials, 2015, 5(21): 1500400.
[4] Higgins D, Zamani P, Yu A P, et al. The application of graphene and its composites in oxygen reduction electrocatalysis: A perspective and review of recent progress[J]. Energy & Environmental Science, 2016, 9(2): 357-390.
[5] Chen K, Song S, Liu F, et al. Structural design of graphene for use in electrochemical energy storage devices[J]. Chemical Society Reviews, 2015, 44(17): 6230-6257.
[6] Raccichini R, Varzi A, Passerini S, et al. The role of graphene for electrochemical energy storage[J]. Nature Material, 2015, 14(3): 271-279.
[7] Lv W, Li Z J, Deng Y Q, et al. Graphene-based materials for electrochemical energy storage devices: Opportunities and challenges[J]. Energy Storage Materials, 2016, 2: 107-138.
[8] ZHANG Qiang, CHENG Xin-bing, HHUANG Jia-qi, et al. Review of carbon materials for advanced lithium-sulfur batteries[J]. New Carbon Materials, 2014, 29(4): 241-264.
(张 强, 程新兵, 黄佳琦, 等. 碳质材料在锂硫电池中的应用研究进展[J]. 新型炭材料, 2014, 29(4): 241-264.)
[9] John D L, Castro L C, Pulfrey D L. Quantum capacitance in nanoscale device modeling[J]. Journal of Applied Physics, 2004, 96(9): 5180-5184.
[10] Stoller M D, Magnuson C W, Zhu Y W, et al. Interfacial capacitance of single layer graphene[J]. Energy and Environmental Science, 2011, 4: 4685-4689.
[11] Uesugi E, Goto H, Eguchi R, et al. Electric double-layer capacitance between an ionic liquid and few- layer graphene[J]. Scientific Reports, 2013, 3: 1595-1601.
[12] Sharma R, Baik J H, Perera C J, et al. Anomalously large reactivity of single graphene layers and edges toward electron transfer chemistries[J]. Nano Letters, 2010, 10(2): 398-405.
[13] Sharma R, Nair N, Strano M S. Structure-reactivity relationships for graphene nanoribbons[J]. The Journal of Physical Chemistry C, 2009, 113(33): 14771-14777.
[14] Mccreery R L. Advanced carbon electrode materials for molecular electrochemistry[J]. Chemical Reviews, 2008, 108: 2646-2687.
[15] Heller I, Kong J, Williams K A, et al. Electrochemistry at single-walled carbon nanotubes: The role of band structure and quantum capacitance[J]. Journal of the American Chemical Society, 2006, 128(22): 7353-7359.
[16] Denis P A, Iribarne F. Comparative study of defect reactivity in graphene[J]. The Journal of Physical Chemistry C, 2013, 117(37): 19048-19055.
[17] Banhart F, Kotakoski J, Krasheninnikov A V. Structural defects in graphene[J]. ACS Nano, 2011, 5(1): 26-41.
[18] Meyer J C, Kisielowski C, Erni R, et al. Direct imaging of lattice stoms and topological defects in graphene membranes[J]. Nano Letters, 2008, 8(11): 3582-3586.
[19] Ma J, Alfe′D, Michaelides, A, et al. Stone-wales defects in graphene and other planar sp2-bonded materials[J]. Physical Review B, 2009, 80(3): 033407.
[20] Chen L, Hu H, Ouyang Y, et al. Atomic chemisorption on graphene with stone-thrower-wales defects[J]. Carbon, 2011, 49(10): 3356-3361.
[21] Krasheninnikov A V, Lehtinen P O, Foster A S, et al. Bending the rules: Contrasting vacancy energetics and migration in graphite and carbon nanotubes[J]. Chemical Physics Letters, 2006, 418(1-3): 132-136.
[22] Hou Z F, Wang X L, Ikeda T, et al. Electronic structure of N-doped graphene with native point defects[J]. Physical Review B, 2013, 87(16): 165401.
[23] Lee G, Wang C Z, Yoon E, et al. Diffusion, coalescence, and reconstruction of vacancy defects in graphene layers[J]. Physical Review Letters, 2005, 95(20): 205501-205508.
[24] Wu L, Hou T, Li Y, et al. First-principles study on migration and coalescence of point defects in monolayer graphene[J]. The Journal of Physical Chemistry C, 2013, 117(33): 17066-17072.
[25] El-Barbary A A, Telling R H, Ewels C P, et al. Structure and energetics of the vacancy in graphite[J]. Physical Review B, 2003, 68(14): 144107.
[26] Oubal M, Picaud S, Rayez M, et al. Structure and reactivity of carbon multivacancies in graphene[J]. Computational and Theoretical Chemistry, 2012, 990: 159-166.
[27] Oleg V, Steven G. Topological defects in graphene: Dislocations and grain boundaries[J]. Physical Review B, 2010, 81(19): 2498-2502.
[28] Andrey C, Jannik C, Gerardo A, et al. From graphene constrictions to single carbon chains[J]. New Journal of Physics, 2009, 11: 083019.
[29] Wang H, Maiyalagan T, Wang X. Review on recent progress in nitrogen-doped graphene: Synthesis, characterization, and its potential applications[J]. ACS Catalysis, 2012, 2(5): 781-794.
[30] Wang H, Xie M, Thia L, et al. Strategies on the design of nitrogen-doped graphene[J]. The Journal of Physical Chemistry Letters, 2014, 5(1): 119-125.
[31] Guo B, Liu Q, Chen E, et al. Controllable N-doping of graphene[J]. Nano Letters, 2010, 10(12): 4975-4980.
[32] Lin Y, Lin C, Chiu P. Controllable graphene N-doping with ammonia plasma[J]. Applied Physics Letters, 2010, 96(13): 133110.
[33] Imamura G, Saiki K. UV-irradiation induced defect formation on graphene on metals[J]. Chemical Physics Letters, 2013, 587: 56-60.
[34] Akada K, Terasawa T, Imamura G, et al. Control of work function of graphene by plasma assisted nitrogen doping[J]. Applied Physics Letters, 2014, 104(13): 131602.
[35] Paek E, Pak A J, Kweon K E, et al. On the origin of the enhanced supercapacitor performance of nitrogen-doped graphene[J]. The Journal of Physical Chemistry C, 2013, 117(11): 5610-5616.
[36] Hou Z F, Wang X L, Ikeda T, et al. Interplay between nitrogen dopants and native point defects in graphene[J]. Physical Review B, 2012, 85(16): 165439.
[37] Hou Z, Shu D, Chai G, et al. Interplay between oxidized monovacancy and nitrogen doping in graphene[J]. The Journal of Physical Chemistry C, 2014, 118(34): 19795-19805.
[38] Hou Z, Terakura K. Effect of nitrogen doping on the migration of the carbon adatom and monovacancy in graphene[J]. The Journal of Physical Chemistry C, 2015, 119(9): 4922-4933.
[39] Ren X, Zhu J, Du F, et al. B-doped graphene as catalyst to improve charge rate of lithium-air battery[J]. The Journal of Physical Chemistry C, 2014, 118(39): 22412-22418.
[40] Cueto M, Ocón P, Poyato J M L. Comparative study of oxygen reduction reaction mechanism on nitrogen-, phosphorus-, and boron-doped graphene surfaces for fuel cell applications[J]. The Journal of Physical Chemistry C, 2015, 119(4): 2004-2009.
[41] Zhang L, Niu J, Li M, et al. Catalytic mechanisms of sulfur-doped graphene as efficient oxygen reduction reaction catalysts for fuel cells[J]. The Journal of Physical Chemistry C, 2014, 118(7): 3545-3553.
[42] Paek E, Pak A J, Hwang G S. A computational study of the interfacial dtructure and capacitance of graphene in [BMIM][PF6] ionic liquid[J]. Journal of The Electrochemical Society, 2013, 160(1): A1-A10.
[43] Pak A J, Paek E, Hwang G S. Tailoring the performance of graphene-based supercapacitors using topological defects: A theoretical assessment[J]. Carbon, 2014, 68: 734-741.
[44] Yang G M, Zhang H Z, Fan X F, et al. Density functional theory calculations for the quantum capacitance performance of graphene-based electrode material[J]. The Journal of Physical Chemistry C, 2015, 119(12): 6464-6470.
[45] Wood B C, Ogitsu T, Otani M, et al. First-principles-inspired design strategies for graphene-based supercapacitor electrodes[J]. The Journal of Physical Chemistry C, 2014, 118(1): 4-15.
[46] Biener J, Stadermann M, Suss M, et al. Advanced carbon aerogels for energy applications[J]. Energy & Environmental Science, 2011, 4(3): 656-667.
[47] Kim K, Lee Z, Malone B D, et al. Multiply folded graphene[J]. Physical Review B, 2011, 83(24): 245433.
[48] Pak A J, Paek E, Hwang G S. Impact of graphene edges on enhancing the performance of electrochemical double layer capacitors[J]. The Journal of Physical Chemistry C, 2014, 118(38): 21770-21777.
[49] Pi K, McCreary K M, Bao W, et al. Electronic doping and scattering by transition metals on graphene[J]. Physical Review B, 2009, 80: 075406.
[50] Kim G, Jhi S, Lim S, et al. Effect of vacancy defects in graphene on metal anchoring and hydrogen adsorption[J]. Applied Physics Letters, 2009, 94: 173102.
[51] Paek E, Pak A J, Hwang G S. Large capacitance enhancement induced by metal-doping in graphene-based supercapacitors: A first-principles-based assessment[J]. Acs Applied Materials & Interfaces, 2014, 6(15): 12168-12176.
[52] Su F Y, You C H, He Y B, et al. Flexible and planar graphene conductive additives for lithium-ion batteries[J]. Journal of Materials Chemistry, 2010, 20(43): 9644-9650.
[53] LI Yong, LU Xiao-hui, SU Fang-yuan, et al. A graphene/carbon black hybrid material: a novel binary conductive additive for lithium-ion batteries[J]. New Carbon Materials, 2015, 30(2): 128-132.
(李 用, 吕小慧, 苏方远等. 石墨烯/炭黑杂化材料: 新型、高效锂离子电池二元导电剂[J]. 新型炭材料, 2015, 30(2): 128-132.)
[54] Mapasha R E, Chetty N. Ab initio studies of staggered Li adatoms on graphene[J]. Computational Materials Science, 2010, 49(4): 787-791.
[55] Medeiros P V C, Mota F D B, Mascarenhas A J S, et al. Bonding character of lithium atoms adsorbed on a graphene layer[J]. Solid State Communications, 2011, 151(7): 529-531.
[56] Zhou L, Hou Z F, Wu L. First-principles study of lithium adsorption and diffusion on graphene with point defects[J]. The Journal of Physical Chemistry C, 2012, 116(41): 21780-21787.
[57] Zheng J, Ren Z, Guo P, et al. Diffusion of Li+ ion on graphene: A DFT study[J]. Applied Surface Science, 2011, 258(5): 1651-1655.
[58] Wang X, Zeng Z, Ahn H, et al. First-principles study on the enhancement of lithium storage capacity in boron doped graphene[J]. Applied Physics Letters, 2009, 95(18): 183103.
[59] Martinez J I, Cabria I, Lopez M J, et al. Adsorption of lithium on finite graphitic clusters[J]. Journal of Physical Chemistry C, 2009, 113(3): 939-941.
[60] Uthaisar C, Barone V, Peralta J E. Lithium adsorption on zigzag graphene nanoribbons[J]. Journal of Applied Physics, 2009, 106(11): 113715.
[61] Denis P A. Chemical reactivity of lithium doped monolayer and bilayer graphene[J]. Journal of Physical Chemistry C, 2011, 115(27): 13392-13398.
[62] Gao S H, Ren Z Y, Wan L J, et al. Density functional theory prediction for diffusion of lithium on boron-doped graphene surface[J]. Applied Surface Science, 2011, 257(17): 7443-7446.
[63] Krepel D, Hod O. Lithium adsorption on armchair graphene nanoribbons[J]. Surface Science, 2011, 605(17-18): 1633-1642.
[64] Wu D H, Li Y F, Zhou Z. First-principles studies on doped graphene as anode materials in lithium-ion batteries[J]. Theoretical Chemistry Accounts, 2011, 130(2-3): 209-213.
[65] Garay-Tapia A M, Romero A H, Barone V. Lithium adsorption on graphene: From isolated adatoms to metallic sheets[J]. Journal of Chemical Theory and Computation, 2012, 8(3): 1064-1071.
[66] Sun C H, Searles D J. Lithium storage on graphdiyne predicted by DFT calculations[J]. Journal of Physical Chemistry C, 2012, 116(50): 26222-26226.
[67] Zhou J J, Zhou W W, Guan C M, et al. First-principles study of lithium intercalated bilayer graphene[J]. Science China-Physics Mechanics & Astronomy, 2012, 55(8): 1376-1382.
[68] Buldum A, Tetiker G. First-principles study of graphene-lithium structures for battery applications[J]. Journal of Applied Physics, 2013, 113(15): 154312.
[69] Luo G X, Zhao J J, Wang B L. A theoretical evaluation of the effect of interlayer spacing and boron doping on lithium storage in graphite[J]. Computational Materials Science, 2013, 68: 212-217.
[70] Lee E, Persson K A. Li absorption and intercalation in single layer graphene and few layer graphene by first principles[J]. Nano Letters, 2012, 12(9): 4624-4628.
[71] Fan X F, Zheng W T, Kuo J L, et al. Adsorption of single Li and the formation of small Li clusters on graphene for the anode of Lithium-Ion batteries[J]. Acs Applied Materials & Interfaces, 2013, 5(16): 7793-7797.
[72] Liu Y, Artyukhov V I, Liu M, et al. Feasibility of lithium storage on graphene and its derivatives[J]. J Phys Chem Lett, 2013, 4(10): 1737-1742.
[73] Datta D, Li J W, Koratker N, et al. Enhanced lithiation in defective graphene[J]. Carbon, 2014, 80: 305-310.
[74] Ma C C, Shao X H, Cao D P. Nitrogen-doped graphene nanosheets as anode materials for lithium ion batteries: a first-principles study[J]. Journal of Materials Chemistry, 2012, 22(18): 8911-8915.
[75] Yildirim H, Kinaci A, Zhao Z J, et al. First-principles analysis of defect-mediated Li adsorption on graphene[J]. Acs Applied Materials & Interfaces, 2014, 6(23): 21141-21150.
[76] Fan X, Zheng W T, Kuo J. Adsorption and diffusion of Li on pristine and defective graphene[J]. Acs Applied Materials & Interfaces, 2012, 4(5): 2432-2438.
[77] Zhou L J, Hou Z F, Wu L M, et al. First-principles studies of lithium adsorption and diffusion on graphene with grain boundaries[J]. Journal of Physical Chemistry C, 2014, 118(48): 28055-28062.
[78] Yao F, Gunes F, Ta H Q, et al. Diffusion mechanism of lithium ion through basal plane of layered graphene[J]. Journal of the American Chemical Society, 2012, 134(20): 8646-8654.
[79] Zhou L, Hou Z F, Wu L, et al. First-principles studies of lithium adsorption and diffusion on graphene with grain boundaries[J]. The Journal of Physical Chemistry C, 2014, 118: 28055-28062.
[80] Kattel S, Wang G. Reaction pathway for oxygen reduction on FeN4 embedded graphene[J]. The Journal of Physical Chemistry Letters, 2014, 5(3): 452-456.
[81] Boukhvalov D W, Son Y. Oxygen reduction reactions on pure and nitrogen-doped graphene: a first-principles modeling[J]. Nanoscale, 2012, 4(2): 417-420.
[82] Zhang L, Xia Z. Mechanisms of oxygen reduction reaction on nitrogen-doped graphene for fuel cells[J]. The Journal of Physical Chemistry C, 2011, 115(22): 11170-11176.
[83] Zhang L, Niu J, Dai L, et al. Effect of microstructure of nitrogen-doped graphene on oxygen reduction activity in fuel cells[J]. Langmuir, 2012, 28(19): 7542-7550.
[84] Jiao Y, Zheng Y, Jaroniec M, et al. Origin of the electrocatalytic oxygen reduction activity of graphene-based catalysts: A roadnnap to achieve the best performance[J]. Journal of the American Chemical Society, 2014, 136(11): 4394-4403.
[85] Lim D, Negreira A S, Wilcox J. DFT Studies on the interaction of defective graphene-supported Fe and Al nanoparticles[J]. The Journal of Physical Chemistry C, 2011, 115(18): 8961-8970.
[86] Lim D, Wilcox J. DFT-based study on oxygen adsorption on defective graphene-supported Pt nanoparticles[J]. The Journal of Physical Chemistry C, 2011, 115(46): 22742-22747.
[87] Krasheninnikov A V, Lehtinen P O, Foster A S, et al. Embedding transition-metal atoms in graphene: Structure, bonding, and magnetism[J]. Physical Review Letters, 2009, 102(12): 126807.
[88] Zheng Y, Xiao W, Cho M, et al. Density functional theory calculations for the oxygen dissociation on nitrogen and transition metal doped graphenes[J]. Chemical Physics Letters, 2013, 586: 104-107.
[89] Groves M N, Chan A S W, Malardier-Jugroot C, et al. Improving platinum catalyst binding energy to graphene through nitrogen doping[J]. Chemical Physics Letters, 2009, 481(4-6): 214-219.
[90] Yan H J, Xu B, Shi S Q, et al. First-principles study of the oxygen adsorption and dissociation on graphene and nitrogen doped graphene for Li-air batteries[J]. Journal of Applied Physics, 2012, 112(10): 104316.