薄型丝织物缝口纰裂与其物理性能的关系Yd20103

程淑婉，方丽英 浙江理工大学，浙江杭州310018

收稿日期：2016-08-17

作者简介：程淑婉(1990-)，女，山东菏泽人，硕士研究生。

原载：山东纺织科技2016/5;9-12

【摘要】为了分析薄型丝织物缝口纰裂的影响因素，对9种典型的真丝面料进行了缝口纰裂测试，并运用SPSS软件分析经纬向滑移量与面料各物理性能指标之间的关系，建立了两者的多元回归预测模型。结果表明：总紧度、经纬向紧度和面密度对丝织物经纬向滑移量影响最大；减小丝织物的总紧度、经纬向紧度和面密度有利于改善丝织物的抗纰裂性；多元回归预测模型的精度较高。

【关键词】丝织物；缝口纰裂；物理性能；回归方程；相关性

【中图分类号】TS101.9 文献标识码：A 文章编号：1009-3028(2016)05-0009-04

面料性能影响着服装加工和缝纫质量[1]，其中紧度、经纬密度、织物组织、经纬丝张力及摩擦力等物理性能对纰裂都有影响[2-3]。轻薄、结构疏松的面料，脱丝和破洞等现象十分常见[4]，如丝绸面料，属于长丝织物，经纬纱之间的摩擦力较小，丝织物易发生纰裂，严重影响了服装的外观和质量[5]。目前，国内外学者在缝口纰裂方面做了一些研究，主要包括纤维种类与性能、织物结构、织造工艺与后整理以及织物在使用过程中的受力情况等方面，但对于缝口纰裂客观预测方面研究较少[6-7]。

因此，本文在选取9种典型薄型真丝面料的基础上，测试了丝织物的经纬向滑移量及物理性能，运用SPSS对影响丝织物服装缝口纰裂物理性能的各项指标进行分析，并找出对缝口纰裂影响较大的指标，通过改变该指标的大小来改善丝织物服装的抗纰裂性。通过实验和数据分析，建立了经(纬)向滑移量与面料物理性能各指标的多元回归预测模型，为企业在选购面料时提供帮助。

1 纰裂实验

1.1 纰裂定义

纰裂是织物在使用过程中某些部位因受力(如摩擦力、弯曲力等)作用而发生经纬纱相对滑移的现象，经纱垂直于受力方向，沿纬纱方向滑移，即纬向纰裂或经纱纰裂；纬纱垂直于受力方向，沿经纱方向滑移，即经向纰裂或纬纱纰裂[8]。

1.2 缝口纰裂实验

由于缝口纰裂直接影响到服装的美观和质量，而不同面料的经纬向滑移量与面料的性能有很大的关系。因此，要减小滑移量，必须找出经纬向滑移量与面料各物理性能参数之间的数学关系。进行纰裂实验后得出每块面料的经纬向滑移量，分析发现纬向滑移量大于经向滑移量，经纬向实验各重复5次取平均值。

1.2.1 实验设备与材料

实验设备为工业缝纫机和3365型Instron万能材料试验机；实验材料为从市场上随机选取的9种典型的真丝面料，试样尺寸为200 mm×100 mm，经向和纬向各5块。

1.2.2 实验方法和结果

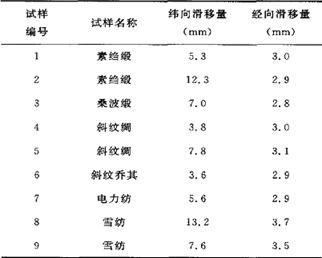
参照GB／T 13772.2-2008《纺织品机织物接缝处纱线抗滑移的测定第2部分定负荷法》[9]裁剪试样，缝制试样时，缝纫线选择40 tex 100涤纶包芯纱；机针选用11号；缝迹密度为15针／3cm，缝纫机型号为QY-9900B，实验过程全部由一人独立完成，按照测试标准设定拉伸速度为50mm／min，夹持距离为10 cm，夹持尺寸为(25 mm±1 mm)×(25 mm±1mm)的试样，测得经纬向滑移量的数据，见表1。

2 面料性能测试实验

2.1 实验设备

表1 丝织物经纬向纰裂值测试结果

注：滑移量为每组实验重复5次的平均值。

YG(B)141D数字式织物厚度仪、XY系列精密电子天平、织物密度镜、显微镜。

2.2 实验结果

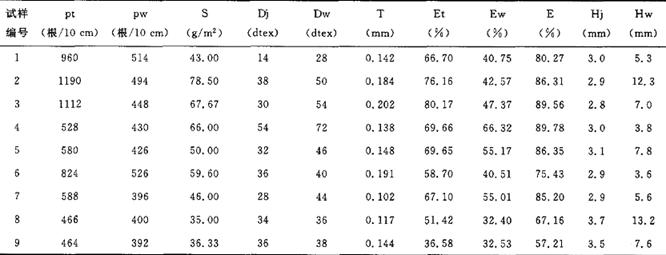
影响丝织物服装缝口经纬向滑移量的物理性能指标主要有：厚度、面密度、经纬向密度、经纬向紧度、总紧度、经纬向细度等。依照GB／T13772.2-2008《纺织品机织物接缝处纱线抗滑移的测定第2部分定负荷法》对9种丝织物物理性能进行测试，再结合表1中经纬向滑移量，得到表2，其中各项性能及滑移量均取5块试样平均值。表2中各项性能及其单位为：厚度T：mm，面密度S：g／m2，经纬密度pt、pw：根／10 cm，经纬向细度Dj、Dw：dtex，经纬向紧度Et、Ew：%，总紧度E：%，经纬向滑移量：Hj、Hw：mm。

表2 面料物理性能与经纬向滑移量的测试结果

3 数据处理与分析

3.1 滑移量与物理性能指标的回归分析

缝口纰裂是服装在服用过程中，受到外作用力而使经纬纱发生相对滑移的现象，织物物理性能对缝口纰裂有一定影响。通过SPSS软件的多元回归分析方法，研究并建立丝织物物理性能指标与滑移量的回归方程[10]。回归方程的自变量为表2中所测试的厚度T，面密度S，经纬向密度pt、pw，经纬向细度Dj、Dw，经纬向紧度Et、Ew，总紧度E；因变量为经向滑移量Hj和纬向滑移量Hw，在置信度区间95%条件下，建立的多元回归方程如下：

Hj＝5.135－0.068E十0.061Et＋0.028Dj－0.027S (1)

Hw =18.903－0.017pw－0.108Ew (2)

由(1)和(2)式可以看出，丝织物的经、纬向滑移量可由其物理性能指标的回归方程计算得到，且表2中的总紧度E、经向紧度Et、经向细度Dj、面密度S出现在回归方程(1)式，而纬向密度pw和纬向紧度Ew 出现在回归方程(2)式。说明总紧度E、经向紧度Et、经向细度Dj、面密度S与经向滑移量Hj有关；纬向密度pw 和纬向紧度Ew与纬向滑移量Hw有关。

在回归模型的建立方法中，本文纰裂实验选择了向后法，即首先让所有的自变量进入回归方程，然后再逐一消除它们的方法。删除变量是以选项对话框中设定的F概率值为参考标准的，在删除的过程中，和因变量之间显著性水平最大的自变量首先被删除，直到回归方程中再也没有满足删除条件的自变量为止[10]。

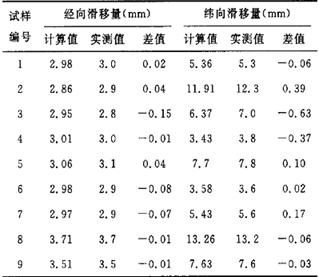
3.2 滑移量与面料物理性能指标回归方程验证将式(1)、(2)计算得到的经纬向滑移量与实澳0值进行比较，以验证回归方程(1)和(2)的精确性和可行性，结果见表3。表3中经向滑移量公式计算值是将总紧度E、经向紧度Et、经向细度、面密度s代入式(1)计算所得，实测值为表1中经向滑移量；表3中纬向滑移量公式计算值是将纬向密度pw 和纬向紧度Ew代入式(2)计算所得，实测值为表1中纬向滑移量。

表3 滑移量公式计算值与实测值对比表(mm)

由表3中数据可以看出，式(1)和(2)中计算所得的经向滑移量与实测值差异很小，除了5号试样计算值与实测值差距较大以外(可看做是异常值)，其他试样计算值与实测值差距均未超过0.7 mm。因此，可认为采用式(1)和(2)比较精确地计算出经纬向滑移量。这也说明式(1)和(2)中包含的物理性能指标基本涵盖了所有与经纬向滑移量有关的物理性能指标，因此这两个方程具有较高的精度和实用价值。

3.3 滑移量与物理性能指标的相关性分析

为了深入研究丝织物易发生缝口纰裂的实质，并找出对滑移量影响较大的物理性能指标，以便提高丝织物的抗纰裂性，本文分析了丝织物滑移量与其物理性能指标的相关性。通过数据分析，得到丝织物各物理性能指标与滑移量的相关性由低到高如下(其中数字代表pearson相关性系数)：

经向：Dj=0.076<Dw=0.377<T=0.490< pw=0.555< Ew=0.562< pt=0.668< S=0.73O< Et=0.80l< E=0.809

纬向：Dj=0.180<T=0.320<pt=0.426<Pw=0.491< Dw=0.566< S=0.678< Et=0.694< Ew =0.726< E=0.783

由以上丝织物各物理性能指标与经纬向滑移量的相关性分析可以看出：(1)总紧度E、经向紧度Et、纬向紧度Ew、面密度S对丝织物的经纬向滑移量影响较大，且E、Et、Ew、S越大，滑移量越小，丝织物抗纰裂性越好；(2)经密pt、纬密pw、纬向细度Dw、厚度T对丝织物的经纬向滑移量影响次之；(3)经向细度对丝织物经纬向滑移量影响最小。

基于上述几点可知，提高丝织物的抗纰裂性可以从改善其总紧度、经纬向紧度、面密度着手，减小丝织物的总紧度、经纬向紧度和面密度有利于改善丝织物的抗纰裂性。

4 结论

1、丝织物受到拉伸变形时，纬向纰裂值远远大于经向纰裂值，即经纱更易沿着纬纱方向发生纰裂现象。

2、通过分析丝织物滑移量与其物理性能指标的相关性，发现总紧度E、经向紧度Et、纬向紧度Ew和面密度S对丝织物的经纬向滑移量影响最大，可减小丝织物的总紧度、经纬向紧度和面密度来改善丝织物的抗纰裂性。

3、本文通过实验和数据分析，分别建立了采用丝织物物理性能指标表示丝织物经纬向滑移量的回归方程。经向纰裂实验的回归方程：Hj＝5.135－0.068E+ 0.061Et＋0.028Dj－0.027S；纬向纰裂实验的回归方程：Hw=18.903－0.017pw－0.10BEw。回归方程的计算值与滑移量实测值差距较小，具有一定的实用价值。

参考文献：

[1] 邹奉元,方丽英.丝绸面料缝口性能与缝纫条件的关系[J]纺织学报,2002,23(1);53-55.

[2] 裘愉发.合纤织物的纰裂EJ].上海纺织科技,2008,36(4)32- 33.

[3]Zhu.B,Yu.T.X,Tao.X.M .Large Deformation and Slippage M echanism of Plain woven Com posite in Bias Extension[J].Composites Part A;Applied Science and Manufacturing,2007,38(8);1821 1828.

[4]金美菊,石东亮,洪武勇.服装纰裂程度测试方法探讨[J].上海纺织科技,2011,39(10);26-27.

[5]黄莉茜,张艳峰.织物纰裂性能分析[J].上海纺织科技,2002,30(1);55- 56.

[6]钱有清,赵娟,左保齐.桑蚕丝平纹织物的纰裂性能[J].纺织学报,2O10,315(5);38-43.

[7] Baoqi Zuo,Juan Zhao,Feng Zhang,et a1.Study for the Method of Slippage of Silk Fabric[J].Textile Bioengineering and Informatics Symposium Proceeding,2008,(2);186-190.

[8] 乔敏.涤纶长丝织物纰裂性能研究[D].上海;东华大学,2012.

[9] GB／T 13772.2-2008纺织品机织物接缝处纱线抗滑移的测定第2部分定负荷法[s].北京;中国标准出版社,2008.

[10] 沈渊.SPSS17.0统计分析及应用实验教程[M].浙江;浙江大学出版社,2013.