消防服衣下空气层热传递机制研究进展yd19331
苏云,王云仪,李俊 1、东华大学服装艺术设计学院,上海200051;2、东华大学功能防护服装研究中心,上海20005;3、现代服装设计与技术教育部重点实验室,上海200051)
收稿日期:2015-01-27 修回日期:2015-08-22
基金项目:国家自然科学基金资助项目(51576038);人因工程国家重点实验室开放课题(SYFD150051812K);中央高校基本科研业务费专项基金资助项目(15D110735/36)
作者简介:苏云(1990-),男,博士生。研究方向为功能防护服装。王云仪,通信作者,E-mail:wangyunyi@dhu.edu.cn。
原载:纺织学报2016/1;167-172
【摘要】空气层热湿传递机制的研究不仅可为更加准确的实验室热防护性能测试提供指导,也可提高消防服热湿传递数值模拟的精确度。在阐述了热防护性能测试中空气层的作用以及空气层热传递机制和空气层热传递模型的研究现状的基础上,分析了服装与人体之间空气层微气候的特征,从热传导、对流换热和辐射换热3个方面总结了空气层的热传递机制,提出不同条件下空气层传热模型建立的基本思路,并对未来消防服衣下空气层热传递机制的研究动向作出了预测。
【关键词】消防服;空气层;热传递;数值模拟
【中图分类号】:X 924.3;TS 941.73 文献标志码:A DOI:10.13475/j.fzxb.20150105306
对于参与紧急灭火的消防员而言,热应力是其生命安全和身心健康的最大威胁。这种恶劣环境通常可以被划分为普通、危险、紧急3种状态[1]。紧急状态常常发生在闪火环境下,热流密度达到20~209.34 kW/m2,消防员的耐受时间仅仅只有几秒钟,具有致命的危险[1]。普通和危险状态是属于低水平热辐射环境,热流密度为5~20 kw/m2[2],暴露时间较长,一般没有造成消防服外层面料的热降解,然而实际情况中消防员的皮肤烧伤较多发生在这种环境条件下[3-4]。消防服作为高温下使用的防护性服装,能够减少或防止皮肤烧伤,提高消防作战效率。其热防护性能的好坏,直接关系到作业人员的安危,因此,准确评价服装的热防护性能,在不同场合选择合适的消防服具有重要意义。然而,服装各层的空气层是评价与改善服装热防护性能的关键因素。
目前热防护性能的各种实验测试方法中,许多学者对于测试中是否需要在传感器与面料之间设置空气层,以及其大小的设置产生了兴趣。在许多小尺度台式测试中,如NFPA 1971《建筑物火灾用灭火防护服标准》规定的闪火条件下的TPP测试、NFPA1977《荒地灭火用防护服和设备标准》规定的21 kW/m2辐射强度下的RPP测试以及美国材料实验协会标准:F 2731-201l《测定消防员防护服系统的能量传播和储存的标准试验方法》规定的8.5 kW/m2辐射强度下的SET测试等,都没有考虑传感器与面料之间空气层的影响。也有测试标准中,如ASTM D4108《热防护性能测试(TPP)》等,规定传感器与面料之间的空气层厚度为6.4 mm,用来模拟服装与人体皮肤之间的间距大小。由于人体体表形状的复杂性,服装覆盖在人体表面形成的衣下空气层分布不均匀,小尺度台式测试并不能准确地模拟着装人体衣下空气层的分布,因此,文献[5-7]利用三维人体扫描仪调查了燃烧假人衣下空气层的分布状况,结果表明,在肩部、前胸、大腿、膝盖等部位形成的空气层较小,在后背较低部位、腰、后膝和小腿的空气层相对较大。同时由于人体的运动以及面料的热收缩导致衣下空气层的动态变化,都预示着全尺度假人实验的必要性[8-9]。
由于空气层传热的复杂性,实验室测量并不能有效解释空气层传热的机制,因此,不少研究学者进行了消防服衣下空气层热传递数值模拟的研究。早期Torvi等[10]基于小尺度台式测试,分析了面料与传感器之间空气层的一维热传递,但是忽略了空气对辐射传热的影响以及各传热方式的耦合现象。由于人体几何形态的复杂性,Zhu等[11]基于Torvi建模理论,建立了圆柱坐标系下的空气层传热模型,用以研究不同曲面下空气层的热传递过程。Sawcyn等[12]基于阻燃面料背面温度的梯度分布,建立了空气层的准二维热传递模型,同时Talukdar等[13]副利用CFD(计算机流体动力学,Computational FluidDynamics)技术再现了空气层的多维热传递现象。为了研究空气层的耦合传热以及动态空气层的传热,Ghazy等建立了单层面料空气层传导与辐射热传递耦合模型[14-15]、多层面料多层空气层模型以及人体运动、面料热收缩引起的动态空气层模型[16],以及人体运动、面料热收缩引起的动态空气层模型[17-18],但是,由于衣下空气层厚度的跨度较大,不同火场环境下空气层模拟的差异性,目前衣下空气层数值模拟的精确度以及应用性仍有待提高。
空气层在“人体-服装-环境”的数值模拟中起着桥梁的作用,同时空气层的热传递过程容易受到其他因素的影响,因此,准确分析空气层的热传递机制,对于实验室测试中空气层厚度的设置、不同火场环境条件下空气层热传递模型的建立具有重要意义。本文分析了服装与人体之间空气层微气候的特点,总结了空气层对流、传导以及辐射的传热机制,比较了目前各空气层热传递模型的优缺点,并总结了其未来发展的趋势。
1 空气层微气候
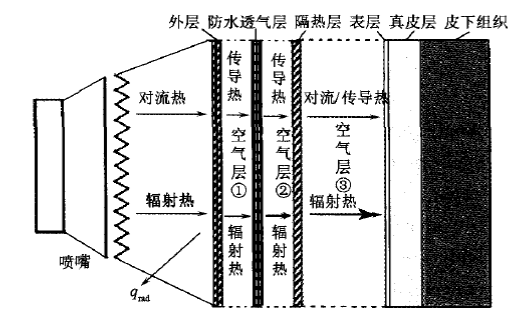
按照NFPA 1971《建筑物火灾用灭火防护服标准》规定,消防服由多层织物系统构成,依次为外层、防水透气层以及隔热层,人体的皮肤结构从外向内依次为表皮层、真皮层、皮下组织,从而形成多层垂直空气层的分布,如图1所示。
|
|
|
图1 消防服的多层面料系统与热传递过程 |
在消防员的消防作业过程中,由于人体的运动以及面料的热动力现象,使得人体一服装一环境之间的热湿传递过程处于动态变化之中[19]。衣下空气层内也不可能完全静止,在隔热层与皮肤表层之间(空气层③),由于存在温度差产生的传导与辐射热传递的同时,也必然会由于空气分子的运动产生自然对流现象,除非衣下空气层所处的空问非常狭小,无法形成对流运动,这时才会有单纯的导热现象(空气层①与空气层②),所以,空气层微气候中同时存在对流、传导、辐射传热以及由于浓度差、温度差、压力差产生的蒸发散热现象。
2 空气层热传递机制
服装与人体之间空气层的热传递过程受多种因素的影响,在空气层中进行热交换的方式有热传导、对流换热和辐射换热,其中热传导和对流换热的计算过程相对简单,而辐射换热比较复杂,但是三者之问具有耦合作用,共同决定着空气层的热传递过程。
2.1 对流/传导热传递
静止空气的导热系数明显小于常见的纺织材料,是理想的绝缘体。随着空气层厚度的增加,空气层导热减小,相反自然对流愈益明显。传热学中利用Ra(瑞利数,Rayleigh number)的大小判断自然对流的发生与否,如下式[20]所示:
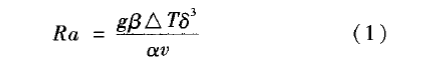
式中:g为重力加速度,9.81 m/s2; 为空气的热膨胀系数,K-1;△T为空气层边界的温度差,K;δ为空气层厚度,m;α为空气热扩散系数,m2/s;v为空气动力黏度,m2/s。
对于处于水平方向的空气层来说,当Ra值达到1 708时,空气层发生稳态自然对流;当Ra值超过5 830时,便会产生非稳态自然对流[21]。然而,Ra值的大小与空气层的厚度呈正比,Torvi利用流动可视化与数值模拟的方法推导出当空气层的厚度达到6.4 mm时出现自然对流[10]。同时由于人体衣下空气层的体积较小,空气层厚度为19.1 mm时的Ra值小于35 000,而发生湍流的Ra值大于106,故衣下空气层的对流换热一般当作层流处理[22]。
2.1.1 传导热传递
当面料与传感器之间空气层厚度小于6.4 mm时,由于空气层间隙太小,从而无法形成对流运动,这时空气层的热传递以传导为主。根据傅里叶热流定律,一维平面的热传导速率方程为
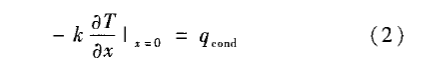
式中:qcond为传导热流密度,W/m2;k为空气层的导热系数,w/(m·K);аT/аx为沿x方向的温度梯度,K/m。
2.1.2 对流热传递
当空气层厚度超过6.4 mm时,空气含量的增加会导致空气层导热的大幅度减小,相比对流传热来说可以忽略不计。在消防作业中,消防服衣下空气层对流传热不仅仅以自然对流的形式进行,同时由于人体步行等连续动作以及面料的热收缩变化,在衣下空气层中会产生强迫对流,如风箱效应或钟摆效应等,但不论对流传热过程的具体特性如何,均可利用牛顿冷却公式计算空气层的对流换热(如式(3)、(4))。同时对流传热是由浮升力引起,这种浮升力是因流体中的温度差所导致,与空气层所处的方向有一定的联系,见式(5)[22-23]。

式中:[]*是指如果方括号内为负值,则此项为0;q conv为对流热流密度,W/m2;h为空气层的对流传热系数,w/(m2·K);Tfab为隔热层背面温度,K;Tskin为皮肤表层温度,K;Nu为努塞尔数;L为空气层的厚度,m。
2.2 辐射热传递
有研究表明,面料与传感器之间空气层的热传递以辐射热交换为主[10],所以准确评价空气层辐射热传递过程,对于提高空气层热传递模型具有重要意义。在消防作业的过程中,服装以及人体皮肤都会向空气层发射热辐射,同时由于空气中02以及N2属于非极性气体,不发射辐射,空气中还含有少量的极性分子气体,如CO2、水蒸气等,在很大温度范围内是发射和吸收辐射[24]。综上所述,一般情况下可把空气层简化成透明体,完全透射辐射,此时空气层辐射热传递遵循斯蒂芬一玻尔兹曼定律,利用视角系数建立的辐射模型为
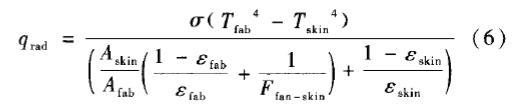
式中:qrad为辐射热流密度,W2/m ;σ为斯蒂芬-玻尔兹曼常数,5.67×10 w/(m2·K4);εfab与εskin分别为面料与皮肤表层的发射率;Afab与Askin分别为面料热暴露与皮肤表层的表面积,m2;Ffab-skin为面料背面发射的辐射被皮肤拦截的比例。
由于面料在高温环境下会发生化学反应,从而产生CO2、颗粒等物质,分布在空气层中,同时消防员高强度作业产生的汗液使空气层的湿度升高,都会增加空气层吸收和发射辐射热。在这种情况下,可以将空气层当作灰体处理,即空气层既能够透过辐射,也能吸收与发射辐射,其空气层进行辐射热传递的计算过程如下:
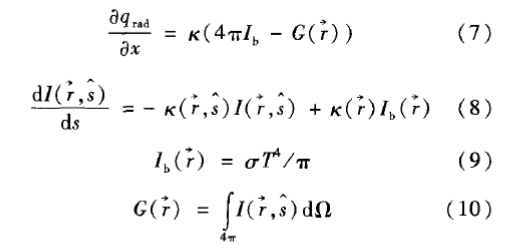
式中:x为空气层的厚度,m;k为空气的吸收系数;Ib为黑体辐射强度,W/m2;s为几何距离,rn;G(r)为入射辐射,W/m2;r→,s⌒分别为空间位置与角方向、
由于以上计算过程复杂,辐射传热模型可进行相关简化。考虑空气层作为辐射介质,但是忽略空气发射辐射,并且通过引进Beer定律,假设空气层吸收热辐射呈指数衰减,其计算方程为
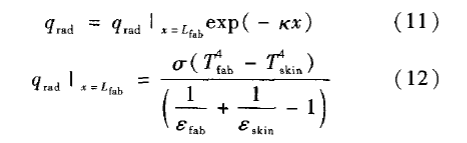
3 空气层传热模型
空气层在“环境一服装一人体”的传热建模中起着关键的作用,因此,建立精确的空气层传热模型对于准确评价服装热防护性能具有重要意义。目前有关消防服空气层的传热模型主要是针对静态空气层的一维传热,它不仅能够揭示空气层传热的基本原理,而且可以为多维空气层、动态空气层的传热模拟奠定理论基础。此外,近几年来部分学者尝试了多维空气层、动态空气层的热传递模拟。
3.1 一维传热模型
Torvi[25]利用有限元方法模拟了ASTM
D4108标准中的TPP测试,分析了织物与传感器之间空气层的对流、传导以及辐射热传递过程,Song[26]和Zhu[27]基于Torvi的空气层传热模型,分别建立了服装与假人皮肤之间的空气层传热模型以及圆柱坐标下的空气层传热模型,但是由于没有考虑各传热之间的耦合以及空气各成分对辐射热传递的影响,与实际情况差异较大。基于对空气层传热机制的研究,改进的空气层一维传热模型为
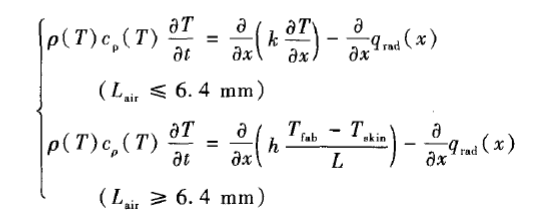
根据上文的分析,标准消防服是多层面料结构,各层面料之间都会存在微小间隙,然而在服装多层系统中不同位置、不同厚度的空气层对服装的热防护性能有不同程度影响[27]。Ghazy等[28]模拟了闪火条件下空气层的传导与辐射热传递,假定服装外层与防水透气层、防水透气与隔热层的空气层厚度均为1 mm,隔热层与传感器的空气层厚度设定为6.35 mm,但是并没有提出隔热层与传感器之间空气层厚度大于6.35 mm的传热方程,其应用范围具有一定的局限性。
3.2 多维空气层传热模型
Torvi[25]建立的一维空气层热传递模型中,当空气层厚度为6.4 mm 时,模型预测结果与实验结果的误差为5% ;而当空气层厚度为12.7~19.1 mm时,预测的误差达到12%~15%,造成较大空气层误差的主要原因是假设空气层为一维热传递。为了进一步提高空气层热传递模拟的精确性,Sawcyn等[12]测量了面料未暴露一侧的温度分布,将面料划分为7个温度场,每个温度场与传感器的辐射热传递分开计算,从而建立了空气层的对流、辐射多维热传递模型,提高了模型预测的精确度。
随着CFD技术的发展,计算机模拟方法具有灵活度高、参数易改变、可重复率高等优点。采用CFD模拟服装与人体之间空气层的多维热传递,能够灵活地设置空气层的多项热物理参数,选择不同的对流传热模型(如Navier-Stokes方程等)和不同的辐射传热模型(如P-1辐射模型等),从而更加准确地评价服装的热防护性能[28]。Talukdar等[13]利用CFD再现了对流传热,假设空气层为透明体介质,利用有限体积法建立辐射传热模型,模拟了面料和传感器间的二维传热,再现了空气层的传热过程。
3.3 动态空气层传热模型
动态空气层的形成,一方面是由于高温条件下面料的热收缩导致空气层厚度的单向变化,另一方面是由于消防员运动导致的空气层厚度的周期性变化。空气层厚度的动态变化会影响空气层的传热方式,尤其是对流传热。Ghazy等[17]通过在空气层模型中引入面料最大热收缩值、收缩率来模拟空气层的动态变化,分析了面料的热收缩变化对服装热防护性能的影响。同时为了分析人体运动产生的空气层变化对热防护性能的影响,Ghazy等[18]在模型中引入了周期性正弦函数,利用空气层变化的振幅与频率研究空气层动态变化对传热的影响。
以上动态空气层模型并没有考虑对流传热过程,这显然与事实不符,并且有学者通过实验证明了人体的运动会导致空气层中强制对流的产生[29],因此,由于面料热收缩以及人体运动产生的空气层变化应该综合考虑对对流、传导、辐射传热的影响。
4 结语
空气层对于服装热防护性能的重要性已经得到大多数研究者的认同。尽管空气层热传递模型的研究取得了快速发展,但是目前空气层热传递的建模条件较理想化,同时由于消防员处于多变的环境中,因此,目前空气层热传递模型的应用具有一定的局限性。未来可以从以下几个方面进行消防服空气层的热传递机制研究。
1)空气层的各向异性热传递机制研究。目前大多数空气层的实验研究都是在小尺度台式测试上进行,空气层处于水平状态,但是消防员实际着装运动过程中,服装与人体之间的空气层是处于垂直状态,2种状态下的空气层热传递存在一定的差异,尤其是对对流传热的影响,这是因为对流传热是由浮升力引起空气的流动而发生。Zhu等[11]已经证明了圆柱坐标系下的垂直空气层发生自然对流的空气层厚度为6 mm,而Torvi等[10]得出的水平方向发生自然对流的空气层厚度为6.4 mm,因此,不同方向空气层的分布势必会影响热量的传递,从而影响服装热防护性能的评价。
2)水分对空气层热传递机制的影响。灭火水枪的喷溅以及消防员高强度运动产生的汗液会导致衣下空气层的相对湿度增加。大量研究结果表明,水分对空气层的热传递有重要影响,在含水面料下空气层发生自然对流的厚度比干态面料大很多,接近9~12 mm[30]。一方面水蒸气是极性分子,能够吸收、发射辐射,影响辐射热传递,另一方面,水蒸气的比热容、导热系数均比空气大,空气层相对湿度的增加会导致空气层的蓄热量增加,热传导速率加快,甚至造成人体皮肤的烫伤,因此,研究不同湿度下空气层的热传递机制,对于准确评价皮肤的烧伤状况有重要意义。
3)不同火场环境下空气层热传递模型研究。
消防员所处的火场环境跨度大,热流密度分布在5~209.34 kW/m 2[1-2]之间,同时对流热与辐射热占比也存在差异。目前建立的空气层热传递模型主要是模拟闪火环境,但是对于低热流密度下(如冷却阶段、长时间远距离低辐射条件等)的空气层热传递模型还未研究,且消防员的皮肤烧伤较多分布在这种环境条件下,因此,研究低热流密度下的空气层热传递机制具有重要意义。
目前空气层热传递机制的研究大多是以水平小尺度台式实验为基础,鉴于与着装人体所形成空气层的分布差异,未来应该进行更多着装人体空气层热传递研究。此外,空气层微气候容易受外界因素的影响,如热源、水分等,因此,研究不同火场环境下空气层的热传递机制具有重要意义。
参考文献
[1]BARKER R L.A review of gaps and 1imitations in test methods for first responder proteefive clothing and equipment[R].[S,1.]:National Personal Protection Technology Laboratory。2005:8-13.
[2]ABBOTT N J,SCHULMAN s.Protection from fire:nonflammable fabrics and coatings[J].Journal of Industrial Textiles,1976,6(1):48-64.
[3]SONG G,PASKALUK S,SATI R,et a1.Thermal protective performance ofprotective clothing used forlow radiant heat protection[J].Textile Research Journal, 2010,81(3):311-323.
[4]SONG G,GHOLAMREZA F,CAO W.Analyzing thermal stored energy and effect on protective performance[J].Textile Research Journal,2011,81(11):1124-i138。
[5]MAH T,SONG G.Investigation of tlIe contribution of garment design to thermal protection:part 1:Characterizing mr gaps using~e-dimensional body scsnning for women’s protective clothing[J]。Textile Research Journal,20lO,80(13);1317-1329.
[6]LU Y,SONG G,LI J.A novel approach forfit analysis of thermal protective clothing using thee-dimensional body scanning[J].Applied Ergonomics,2014(45).1439-1446。
[7]王云仪,张雪,李小辉,等.基于Geomagic软件的燃烧假人衣下空气层特征提取[J]。纺织学报,2012,33(11):102-106.
[8] SONG G.Clothing air gap layers and thermal protective performance in single layer garment[J].Journal of Industrial Textiles,2007,36(3):193-205.
[9] lJl J, LI X, LU Y,et a1. A new approach to characterize the efteet of fabric deformation on thermal protective performance[J].Measurement Science and Technology,2012,23(4):045601.
[10] TORVI D A,DALE J D.FAULKNER B.Influence of air gaps on bench—top test results of flame resistant fabrics[J]. Journal of Fire Protection Engineering,1999,10(1):1-12.
[11] ZHU F,ZHANG W,SONG G. Heat transfer in a cylinder sheathed by flame-resistant fabrics exposed to convective and radiant heat flux[J]. Fire Safety Journal,2008,43(6):401-409.
[12] SAWCYN C M J,TORVI D A.Improving heat transfer models of air gaps in bench top tests of thermal protective fabrics[J].Textile Research Journal,2009,79(7):632-644.
[13] TALUKDAR P,TORVI D A,SIMONSON C J,et a1.Coupled CFD and radiation simulation of air gaps in
bench top protective fabric tests[J].International Journal of Heat and Mass Trans~r,2010,53(1):526-539.
[14] GHAZY A,BERGSTROM D J.Numerical simulation of transient heat transfer in a protective clothing system during a flash fire exposure[J]. Numerical Heat Transfer,Part A:Applications,2010,58(9):702-724.
[15] GHAZY A,BERGSTROM D J.Influence of the air gap between protective clothing and skin on clothing performance during flash fire exposure[J].Heat and Mass Transfer,2011,47(10):1275-1288.
[16] GHAZY A,BERGSTROM D J.Numerical Simulation of heat transfer in firefighters protective clothing with multiple air gaps during flash fire exposure[J].Numerical Heat Trans~r,Part A:Applications,2012,61(8):569-593.
[17] GHAZY A.Influence of thermal shrinkage on protective clothing performance during fire exposure: numerical investigation[J].Mechanical Engineering Research,2014,4(2):1-15.
[18] GHAZY A,BERGSTROM D J.Numerical simulation of the influence of fabric s motion on protective clothing performance during flash fire exposure[J].Heat and Mass Transfer,2013,49(6):775-788.
[19] 张渭源.服装舒适性与功能[M].北京:中国纺织出版社,2005:75-77.
[2O] HOLLANDS K G T,RAITHBY G D,KON1CEK L.Correlation equations for free convection heat transfer in horizontal layers of air and water f J]. International Journal of Heat and Mass Transfer,1975,18(7):879-884.
[21] TORVI D A.DALE J D.Heat transfer in thin fibrous materials under high heat flux[J].Fire Technology, 1999,35(3):210-231.
[22] SAWCYN C M J.Heat transfer model of horizontal air gaps in bench top testing of thermal protective fabrics[D]. Canada: University of Saskatchewan,2003:1-149.
[23] OSTRACH S.Natural convection in enclosures[J].Journal of Heat Transfer,1988,110(4b):1175-1190.
[24] 葛新石,叶宏.传热和传质基本原理[M].6版.北京:化学工业出版社,2007:211-507.
[25] TORVI D A.Heat transfer in thin fibrous materials under high heat flux conditions[D].Edmonton:University of Alberta.1997:1-277.
[26] SONG G W.Modeling thermal protection outfits for fire exposures[D].USA:North Carolina State University,2002:1-209.
[27] FU M,WENG W ,YUAN H.Effects of multiple air gaps on the thermal performance of firefighter protective clothing under low·level heat exposure[J].Textile Research Journal,2014,84(9):968-978.
[28] WANG Y,WANG Z,ZHANG X,et a1.CFD simulation of naked flame manikin tests of fire proof garments[J].Fire Safety Journal,2015,71:187-193.
[29] XIN L,LI X,LI J.A new approach to evaluate the efeet of body motion on heat transfer of thermal protective clothing during flash fire exposure[J].Fibers and Polymers,2014,15(1O):2225-2231.
[30] LU Y,LI J,LI X,et a1.The effect of air gaps in moist protective clothing on protection from heat and flame J].Journal of Fire Sciences,2013,31(2):99-111.