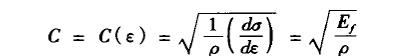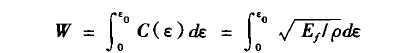防弹层压复合材料防弹效果的理论分析yd18006
熊杰 浙江工程学院,杭州,310033
顾伯洪 王善元 东华大学
教育部科学技术研究重点项目(地方O2O64),浙江省教育厅资助项目(20010771)
原载:纺织学报2003/5;435-437
【摘要】从能量吸收的角度,分析纤维的能量吸收与波传播和纤维与树脂复合效应,可以采用树脂仅存在于平面织物之间,即不渗入到纱线之间以及纤维之间的孔隙的复合方式,而纤维体积分数应大于80% 左右。
【关键词】军需用纺织品 层压复合材料 防弹效果理论分析
【中图分类号】TS 106.6 文献标识码:A
复合材料具有的轻质和高性能使其在弹道防护领域的应用13益拓展。然而迄今为止,防弹复合材料的研制和开发几乎是以经验为依据的,研究者们设计大量的实验要素的组合,然后进行实验测试和比较来获得所需要的防弹复合材料,这种方法不但费时、费力、增加研制成本,实际上也很难获得真正优化的设计制作方案。当然,一种新的防弹材料的研制成功最后必须付诸于实际的测试,但任何一种对复合材料结构设计能够提供指导的方法始终是研究者们努力探求的。本文在Smith[1],Roylance[2],Freeston[3],和Sierakowski[4]等人的研究基础上,对防弹层压复合材料靶板的结构设计进行了理论分析,目的在于在防弹层压复合材料靶板研制过程中缩小实验探索的范围,提高研制的针对性和效率。
1 纤维材料的能量吸收与波传播
层压复合材料的防弹效果与该材料在高应变率(102~l03 /s )下的性能有关,主要取决于在高应变率下该材料的能量吸收能力。在高应变率下层压复合材料的能量吸收能力与组成该复合材料的纤维的断裂应变能密度和在能量吸收过程中参与能量吸收的纤维材料数量密切相关。纤维材料的断裂应变能密度由该纤维应力应变曲线下的面积决定,而参与能量吸收过程的纤维材料数量则由从冲击点发散的冲击波的传播速度决定。为了便于分析,假设:1)纤维在变形时横截面保持平面,沿截面只有均匀的轴向应力。2)与应变率无关,即应力只是应变的单值函数。
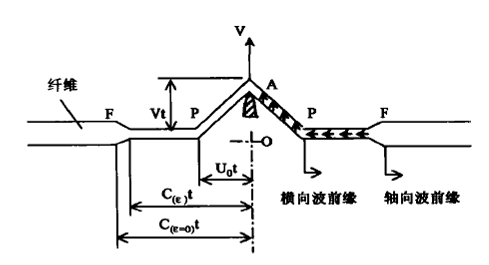
根据Smith[1]对纤维或纱线受横向弹体冲击的分析,结合Freeston[3]等人对织物受弹道冲击时应变波反射的研究,忽略应变波沿纤维轴向传播时所遇到交织点的反射。图1显示了受横向冲击的纤维中波的传播。
弹体的速度为V,冲击引起两个应变的轴向波
|
|
|
图1 受横向冲击的纤维中波的传播 |
向相反方向传播,其速度为C,同时还产生一种横向波,它的形状呈倒V字形,基脚在P点,以速度向两侧传播。在t时,F点以外的纤维质点尚未受到冲击。
对于轴向波传播,相对未变形的质点而言,应变波速度C为:
|
|
(1) |
式中,ρ是纤维密度;dσ/dε 为纤维应力应变曲线的斜率,即为轴向杨氏模量Ef= E(ε),是应变的函数。
对于横向波传播,材料的流动速度为W,即当轴向应变波通过后,APF中质点开始朝反方向收缩的速度,由下式给出
|
|
(2) |
式中,ε。为纤维的最大拉伸应变。在横向波前缘,质点的水平运动停止,并突然以冲击速度
向上(横向)运动,这种横向波向两侧移动的速度相对于未变形的质点而言为U:
|
|
(3) |
式中,σ。为纤维中的最大拉伸应力。因此相对观察者而言,横向波前进速度U。应为:
|
|
(4) |
从图1有:OA=Vt,OP=U0t,AP=(1+ε0)Ut
因此得:
|
|
(5) |
方程(2)~(5)四个方程确立了四对关系,含变量V、W、ε0、σ0、U、U0,其中σ0、ε0、由纤维材料动态应力应变关系确定,已知冲击速度V时,其余四个独立变量W、ε0、U、U0总是可以求得。
假如纤维材料具有线弹性,可求得
|
|
(6) |
由(1)和(6)可以看出轴向波和横向波的传播速度都与C有关,即与纤维材料的模量有关,纤维材料模量越大即C越大,则在一定时间内参与能量吸收的材料数量就越多。
2 复合效应
从弹道防护的要求出发,层压复合材料的综合性能应表现在两个方面:1)高的能量吸收能力;2)结构的刚性和整体性。树脂在平面织物层压复合材料中可能有两种存在的极端情况:第一种情况,树脂不仅存在于平面织物之间,而且渗入到织物的纱线之间以及纱线的纤维之间,即纤维被树脂充分浸渍,树脂在复合材料中呈连续相;第二种情况,树脂仅存在于平面织物之间,不渗入到织物内部,即不渗入到纱线之间以及纤维之间的孔隙。
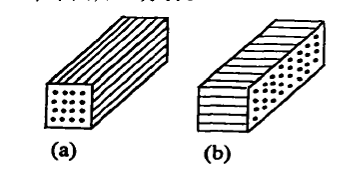
假设在第一种情况下,即纤维材料被树脂充分浸渍,并且不考虑织物交织点的影响。在受到弹体冲击的复合材料靶板中,应力波不仅在靶板平面内传播,而且也沿着靶板厚度方向传播。因此,可以将复合材料靶板看作充满树脂的纤维束集合体。对沿平面内传播和沿厚度方向传播的两种情况取如图2所示的一维单元加以分析。
|
|
|
(a)沿纤维轴向,相应于应力波沿平面内传播 (b)沿纤维横向,相应于应力波沿厚度方向传播 |
|
图2 靶板内应力波传播单元 |
对于图2(a)所示单元,沿单元轴向即沿纤维轴向的波传播速度C由下式给出:
|
|
(7) |
式中,EL是纤维束经树脂浸渍形成的复合材料所具有的轴向等效模量,ρc是复合材料的等效密度。
根据“混合定律”[4],复合材料的弹性模量和密度取决于纤维和基质的模量以及复合材料纤维和基质的相对比例,即体积分数。
|
|
(8) |
|
|
(9) |
式中Vf,Vm分别是纤维和基质的体积分数;Ef,Em分别是纤维和基质的弹性模量;ρf,ρm分别是纤维和基质的密度。因此,沿纤维轴向的波传播速度为:
|
|
(10) |
对于图2(b)所示单元,根据文献[5]可得复合材料横向等效模量Eγ:
|
|
(11) |
式中,
|
|
(12) |
因此,沿该单元轴向即沿纤维横向的应力波传播速度由下式给出:
|
|
(13) |
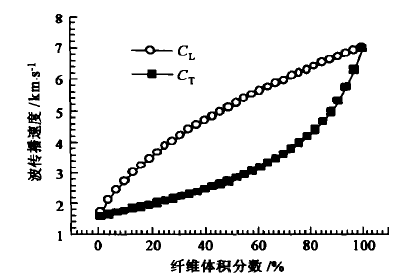
假如纤维采用Twaron标准型,树脂采用酚醛/PVB,则有Ef=70 GPa,Em=3.14 GPa,ρf=1.44 X103 kg/m3,ρm= 1.32 X 103kg/m3, 因此可以得出CL和CT与Vf的关系曲线,如图3所示。
|
|
|
图3 沿纤维轴向和横向的波传播速度与纤维体积分数的关系 |
从图3可以看出,复合材料中沿纤维轴向和横向传播的应力波速度随纤维体积分数的变化关系,复合材料的波传播速度介于纤维和树脂基体的波传播速度之间,纤维体积分数高,则应力波传播速度大,说明纤维与树脂复合以后,纤维的变形受到限制,纤维的波传播速度被抑制。显然,要使复合材料具有高的波传播速度,则应提高纤维的体积分数。然而,过高的纤维含量会导致树脂的量不足以铺展而影响纤维一树脂界面的粘结,从而影响层压复合材料靶板结构的刚性和整体性。由此可以设想在层压复合材料中,要使纤维材料最大限度地保持其波传播能力,又要取得复合材料的刚性和整体性,可以采用第二种复合方式。因此必须仔细控制树脂的含量,以取得复合材料结构的刚性和整体性与弹道性能之间的平衡。就应力波传播的角度来看,从图3可知,沿纤维轴向的波传播速度随纤维体积分数的增加呈平稳上升的趋势,而沿纤维横向的波传播速度随纤维体积分数的变化,在纤维体积分数为80%左右时有一个转折,即当纤维体积分数大于80% 左右时,冲击波传播速度对纤维体积分数的变化较为敏感,因此初步推定纤维体积分数应大于80% 左右。至于纤维含量(或树脂含量)最佳的取值范围,只有根据以上的分析进行实验研究才能确定。
3 结束语
本文在Smith,Roylance,Freeston和Sierakowski等人的研究基础上,从能量吸收的角度,分析了纤维的能量吸收与波传播和纤维与树脂复合效应。初步推断,在层压复合材料中,要使纤维材料最大限度地保持其波传播能力,又要取得复合材料的刚性和整体性,可以采用树脂仅存在于平面织物之间,不渗入到织物内部,即不渗入到纱线之间以及纤维之间的孔隙的复合方式;纤维体积分数应大于80%左右。
致谢:本研究得到中国人民解放军总后军需装备研究所的大力支持,特致谢意!
参考文献
[1] Smith J.C.et a1.Stress-Strain Relationships in Yarns Subjected to Rapid Impact Loading.Part VI:Velocity of Strain Waves Resulting from Impact.T.R.J.,1960(30);752.
[2] David Roylanee et a1.Ballistic Impact of Textile Structures.T.R .J.,1973(1);41~43.
[3] Freeston.W .D .JR .Strain-Wave Reflec tions During Ballistic Impact of Fabric Panels.T.R.J.,1973(6);348-351.
[4] Sierakowski R.L.Dynamic Loading an d Characterization of Fiber-Reinforced Composites.New York;JohnW ileY& Sons.Inc.,1997;15-95.
[5] Ross.C.A .et a1.ElasticW avein Fibe rReinforced Materials.Shock and Vibration Digest,1975(1);96~107.