泡沫物理学史拾萃yd14824

孙其诚， 谭靓慧 1 清华大学水沙科学与水利水电工程国家重点实验室北京100084;2 中国科学院过程工程研究所北京100190

国家自然科学基金(批准号：20776142)、国家人事部留学回国人员择优资助项目(2007年)

收到初稿2007-11-08，收到修改稿2008-03-05

作者通讯：Email：qcsun@ tsinghua．edu．an

原载:《物理》2008/7；473-481

【摘要】人们对泡沫习以为常，却很难理解它的奇特性质，比如几乎完全由空气组成的泡沫，既能像固体一样发生弹性形变，又能像流体一样发生流动，这正是泡沫物理学的研究内容之一．泡沫物理是一门古老的学科，早在19世纪中下叶，气泡和泡沫结构静力学的描述已经完美，之后没有大的发展，直到1990年前后，随着流体力学、微观显像技术和计算技术等学科的发展，以及受材料科学和工业生产的需求，泡沫物理研究再次活跃起来．文章第一作者曾跟随英国皇家学会院士Denis Weaire从事泡沫物理研究多年，在他的演讲和个人收藏中，文章作者积累了一些材料，在此基础上，又仔细查阅了相关文献，整理成此文，它基本概括了泡沫结构静力学发展历程中的重要事件．

【关键词】液态泡沫，泡沫物理学，软物质，水立方

1 泡沫的内在规则结构

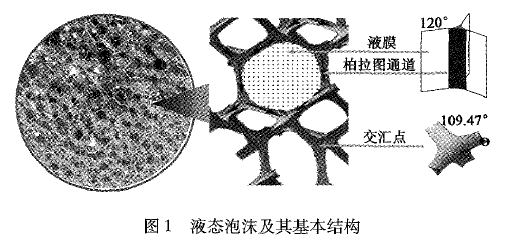
液态泡沫是大量气泡在微量表面活性剂溶液中密集堆积形成的、高度自组织的非平衡系统．平时我们用洗洁精刷洗盘子时，或者从微小开口喷嘴向洗洁精溶液中吹入气体，都能形成泡沫，如图1左侧照片所示。

泡沫表面杂乱无章，内部却具有规则的结构．柏拉图(Joseph A．F．Plateau，1801-1883，比利时物理学家)确定了泡沫结构平衡法则[1]．首先，4个气泡形成一组相互作用的基本单元(气泡大小为10 µm-1cm)，相交于一个交汇点(vertex，junction 或node)；每3个气泡围成一个凹三角形柏拉图通道(plateau border)，则4个气泡共形成4个柏拉图通道，其曲率半径为r_Pb (大小为～1µm-1mm)，它是由液体体积分数、表面张力以及界面力协调决定的．柏拉图通道长度L_Pb约为气泡大小的1／3，柏拉图通道要比交汇点薄一些．每两个气泡间形成一个液膜(film)，4个气泡共形成6个液膜．液膜厚度一般为10Å-1µm，是气泡间的最小分离距离．液膜间以及柏拉图通道间的夹角分别为arc COS(-1／2)=120°和arc COS(-1／3)≈109．47°，图1右侧泡沫照片中的亮白色线就是柏拉图通道。

泡沫中的液体分布在液膜、柏拉图通道和交汇点上，当液体体积分数Φ≈36％时，气泡为圆球状，气泡间的接触缩为一个点，此时液膜消失，仅剩柏拉图通道和交汇点，泡沫的力学特性发生突变，在泡沫物理学的研究中极其重要，因此Φ≈36％称为临界液体体积分数(wet limit)．当Φ>36％时，泡沫系统演变为鼓泡流(bubbly liquid)或者气液两相流(gas／liquid flow)，不再属于泡沫物理的研究范畴。

图1 液态泡沫及其基本结构

早期的泡沫和液膜研究，散见于一些数学家的研究工作中，他们提出了一些重要的思想，并没有做更深入和全面的分析，更没有从物理角度研究这些结构的形成原因．比如，公元四世纪，古希腊几何学家Pappus of Alexandria在《On the sagacity of bees》一文中提到蜜蜂具有理解几何对称的灵性，天生就知道如何用最少量的蜂蜡构建正六边形的蜂巢，紧接着他提出了一系列的思考：蜜蜂如何把平面等分割成等边长单元的呢?对平面而言，为什么只有等三角、等四边、等六边形能周期性的排布成平面，而其他等边形则不行?蜜蜂为什么选择面积恒定时周长最小的正六边形?达尔文(Charles Darwin)曾于1859年创立了著名的进化论，第一次把生物放在科学的基础上．他称赞蜂巢，这是自然界的杰作，在节省材料和劳力方面是完美的(“⋯absolutely perfect in economising labour and wax……”)。

17世纪蓬勃发展的近代科学，强劲地推动了人类对空间结构的不懈探索，比如开普勒猜想(1611)、柏拉图猜想(约1873)、开尔文猜想(约1887)和庞家莱猜想(1904)等著名数学难题，吸引了几代物理学家和数学家共同努力，呕心沥血，力争得到完美解答．其中柏拉图猜想以及受柏拉图工作的启发而提出的开尔文猜想都涉及液膜和泡沫结构问题．1873年柏拉图[2]出版了两卷本书：《Statique Experimentale et Theorique des Liquides soumis aux Seules Forces Moleculaires}，标志着泡沫物理学中的静力学和结构描述已经接近完美．这本书的英文名字为：《Experimental and Theoretical Statics of Liquids：Subject to Molecular Forces Only}。

在此后的近100年间，由于两次世界大战和内战爆发，整个科学研究都受到不同程度的冲击，泡沫物理学也不例外；1950年以后，泡沫物理学的研究虽然恢复生机，但基本上还是延续泡沫或液膜结构的研究，比如物理学家和数学家对开尔文猜想和柏拉图猜想等开展的研究，仅限于局部完善和修补。

2 泡沫静力学和结构法则

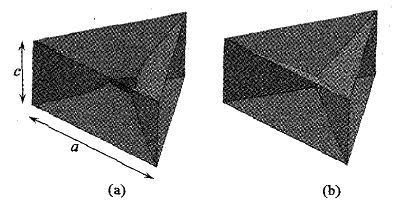
柏拉图曾于1832年发明了诡盘(phenakistis-cope)，制作成动画装置. 28岁时，为了研究视觉暂留效应，直接用肉眼观测太阳，确定闭上眼睛后太阳影像在大脑中的保留时间，结果他只看了十几秒，眼睛就部分失明了．1841年，在他40岁的时候眼睛完全失明，图2是柏拉图的画像.在后来漫长的“黑暗”岁月里，他坚持对肥皂泡薄膜和气泡的几何形态进行研究．他首先设计出一个实验，然后指导他的侄子进行实验，柏拉图再对所得结果进行分析．比如，柏拉图“发现”把线状框架浸入肥皂液中再拿出来时，支架上有一层或多层薄膜．他设计了80多种不同形状的框架，图3是采用Surface Evolver软件重现了柏拉图研究过的液膜形状[3]。

他和他的侄子前后艰难地工作了几十年，把实验现象和分析结果系统整理，1873年出版了著名的法文书：(Statique Experimentale et Theofique des Liquides soumis aux Seules Forces Mol6eulaires)，见图4。

Kenneth Brakke把这本书翻译成英文(www．susqu．edu／facstaff／b／brakke／PlateauBook／PlateauBook．html可下载)。

在这本书中，柏拉图提出了泡沫结构平衡法则，将泡沫结构的研究推向了量化阶段，从这个意义上说，柏拉图开创了泡沫物理学，为以后的研究打下了坚实基础．书名中的Seules Forces Moleculaires有些晦涩，柏拉图的原意是指不考虑重力的影响，液膜和气泡仅在内在分子作用力下发生演变．目前，微重力泡沫实验主要是在国际空间站(Intematioanl Space Station，ISS)，在飞机抛物线飞行(Parabolic flight)时，或者在重力落塔(drop tower)中进行．柏拉图当时缺乏必要的实验条件，不得不采用液液界面强有力的分子间作用力来减弱重力的影响。

图2 柏拉图及其对3气泡排布的研究

图3 边框间的液膜形状(a)上下边框由两个平行的正三角形构成，当两者间距c与三角形边长a的比值较小时，两层液膜间在中间形成三角形的面；(b)当c／a>0.487时，该面不稳定而演变成一条直的柏拉图通道

图4 1873 年出版的柏拉图的《Statique Experimentale et Theorique des Liquides soumis aux Seules Forces Moleculaires)-书第一卷扉页

在思考框架内液膜形态遵循什么法则时，柏拉图认为，稳定的液膜形状应该具有最小面积，这就是液膜面积最小的柏拉图猜想，正如肥皂泡往往是球形的，是因为在给定体积时球形的面积最小，因而也最稳定．柏拉图猜想如同庞家莱猜想、开尔文猜想以及17世纪早期的开普勒猜想一样，一直是物理学家和数学家积极关注和研究的焦点之一．1943年，匈牙利数学家Toth巧妙地证明了在所有首尾相连的多边形中，正多边形的周长是最小的．当多边形的边是曲线时，Toth认为正六边形与其他任何形状的图形相比，它的周长最小，他并不能证明这一点．美国数学家Frank Morgan认为，Toth考虑的多边形边数最多为6，但是从严格数学证明的角度来看，考虑更多的边数更有利于这个问题的最终解决．1976年，美国数学家Jean Taylor和Frederick Almgren得到了柏拉图猜想的数学推导，证明了在最小面积的前提下，当3个液膜连接在一起时，液膜间夹角是120°，4个液膜连在一起夹角为109．47°，但是大家认为，该证明存在不完整和不清晰的部分。

从1992年开始，美国数学家Thomas C．Hales沿着Toth的思路，使用计算机辅助证明了开普勒猜想．经过6年的运算，于1998年8月Hales宣称解决了开普勒猜想，他的整个证明共250页及3Gb的计算机数据，公开放在他的个人网页上让同行验证(http：//www．math．1sa．umich．edu／～hales／)．数学家们普遍认为此次证明的正确性很高，但仍然有待考证．Hales还考虑了周边是曲线时，无论是曲线向外突，还是向内凹，由许多正六边形组成的图形周长为最小，亦即解决了柏拉图猜想．Denis Weaire认为，如果Hales的证明经得起时间的考验，那么这将是杰出的双重成就．

在应用方面，德国建筑师罗尔夫·古特布罗德和弗赖·奥托为1967年在加拿大蒙特利尔举办的世界博览会(Expo’67)设计的德国馆，采用了柏拉图的最小面积猜想，见图5．这是第一次创造性地大规模应用薄膜建筑技术，屋面用特种柔性薄膜材料敷贴，呈半透明状，具有重量轻且空间较大的优点，为世人所瞩目；德国馆的成功启发了1972年慕尼黑奥运会体育场结构和建筑造型的设计。

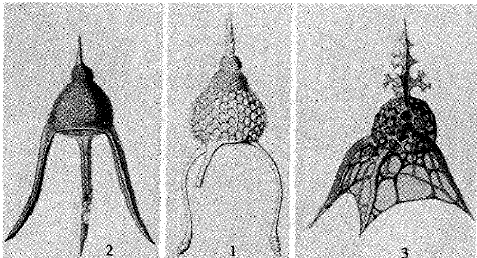
1917年，在剑桥大学出版社出版的达西·汤普森(D’ Arcy Wentworth Thompson)的《On Growth and Form>一书中，把柏拉图提出的表面能最小法则应用到生物学中，从数学和物理学层面分析生命的进程，见图6．当时英国科学的研究正处于顶峰时期，

图5 1967年加拿大蒙特利尔世界博览会(Expo’67)德国馆屋面采用柏拉图猜想进行设计，其屋面表面积最小(a)博览会建筑物全貌；(b)博览会德国馆层顶平面示意图(等高线；比例l／1800)，从屋面等高线可以看出其形状。

这本著作产生了重大的影响，被誉为“既是优美的文学又是高深的科学；既是科学论文，又是娓娓道来的散文”．该书第二版的中文版已经由上海科学技术出版社出版，书名为《生长和形态》．

图6 三种放散虫的骨架结构(D Arey Wentworth Thompson曾用来与气泡结构进行类比)

纵览泡沫物理学发展历程，可以说柏拉图对泡沫的几何表征、力学平衡规则、甚至产生液膜的化学试剂的纯度和浓度做出了全面的科学贡献．不仅如此，这位盲人科学家献身科学的精神得到了同时代物理学界伟人的崇高评价，更为后人所敬仰．

麦克斯韦高度评价了Plateau的工作[4]：“⋯Here we have a book in two volumes，written by a dis—tinguished man of science，and occupied for the most part with the theory and practice of bubble—blowing‘Can the poetry of bubbles survive this?⋯ ”(“⋯ ⋯这里，我们有一本由一位伟大的科学家写的书，这本书共两卷，主要阐述了泡沫的理论和实验研究⋯ ⋯还有比这更好的介绍泡沫之美的诗篇吗?⋯⋯”)；

麦克斯韦[5]‘⋯Which，now，is the more poetical idea——the Etruscan boy blowing bubbles for himself， or the blind man of science teaching his friends to blow them ，and making out by a tedious process of question and answer the condition of the forms and tints that he can never see？ ⋯ ’，“⋯ ⋯ 一个更理想化的情景就是：一个伊特鲁里亚男孩自已用细管吹肥皂泡或一位失明的科学家教他的朋友吹肥皂泡，然后他不断对泡沫的形成结构、色彩的提出问题并从他的朋友那得到回答，以此来展开泡沫的实验研究⋯⋯ ”)；

法拉弟1849年给Plateau的信中说：“⋯Wellmay you and your friends rejoice that though，in the body，you have met with a heavy blow and great dis—couragement，still the spirit makes great compensation，and shines with glorious light across the bodily dark—ness⋯”(引自Tomaso Aste，D．L．Weaire著，The Pursuit of Perfect Packing． London： CRC Press，2000)(“⋯⋯ 你和你的朋友们应该乐于接受这样一个说法，虽然你在身体上承受了巨大的打击和挫折，但是你强大的精神力量弥补了你的身体缺陷，你的思想之光照亮了身体阴霾下的黑暗．⋯⋯”)．

3 开尔文泡沫结构猜想

柏拉图的工作在当时广为流传，威廉姆·汤姆孙(william Thomson，1824-1907)，即以后的开尔文勋爵(Lord Kelvin)深受启发，进而对泡沫空间结构做出了重要贡献，见图7．大家所熟知的是他在电磁学和热力学方面的贡献，比如在1848年提出、在1854年修改的绝对热力学温标．该温标在100年后，亦即于1954年国际会议确定为标准温标．1858年，汤姆孙成功地指导铺设了大西洋海底电缆，因此于1866年被英国王室封为爵士，后又于1892年被授予开尔文勋爵的封号．

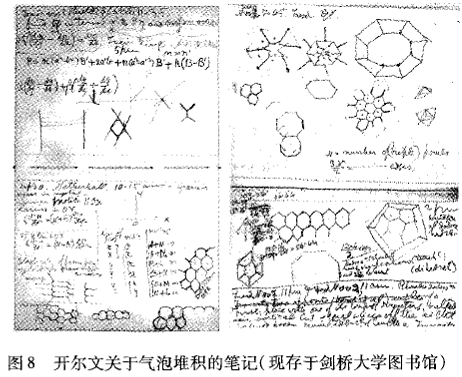
开尔文一生的科学活动是多方面的，对泡沫物理的研究也起了极大的促进作用．19世纪经典物理学基本完善，比如电动机和无线电收发报机的产生，标志着电和磁的研究成果已经绝大多数运用到技术上了．19世纪是探索以太的世纪，当时科学家认为宇宙是由看不见且没有摩擦的连续介质——以太构成，探索以太的存在和性质摆在了当时科学的首要位置，像把“光行差”归之于以太的作用；认为光是靠以太的振动来传播的；认为以太具有刚性，就具有抵抗形状扭曲的能力，以太可以传播横波等都成为当时著名的观点．开尔文则认为以太具有泡沫一样的几何结构，因此他就试图探索完美的泡沫结构应该是什么样的。他认为气泡具有相等的体积，这样就把以太的研究转变为一个纯粹的数学问题：如果把空间分割成大小相同的气泡，在满足柏拉图的结构平衡法则时，面积最小的气泡形态是什么?(What regular partition of space into cells of equal volume has minimal surface area?)．这就是1873年提出的开尔文猜想，把开普勒猜想拓展到泡沫结构的最优堆积上[4]．图8是当时开尔文的研究笔记之一。

图7 开尔文和开尔文单元结构，以及Denis Wemre主编的关于开尔文猜想的专辑(1997)

开尔文还进行了大量实验．开尔文的外甥女Agnes Gardner King在1887年秋天看望开尔文后，这样描述开尔文研究泡沫结构的情形[4]：“⋯Uncle W illiam and Aunt Fanny met me at the door， Uncle W illiam armed with a vessel of soap and glycerine pre—pared for blowing soap bubbles，and a tray with a num—ber of mathematical figures made of wire． These he dips into the soap mixture and a film forms and adheres to the wires very beautifully and perfectly regularly．With some scientific end in view he is studying these films⋯”(“⋯我在门口看到了威廉叔叔和Fanny阿姨，威廉叔叔手拿一个器皿和一个托盘，器皿里装着加了甘油的肥皂水，打算用来吹肥皂泡，托盘里放着数个用金属丝扭成的数学图案．他把这些金属图案在肥皂水里蘸湿后，这些金属丝上就会附着上了液膜，它们的形状非常规整、非常漂亮．他用他科学的思维来研究这些液膜．⋯⋯ ”)．

图8 开尔文关于气泡堆积的笔记(现存于剑桥大学图书馆)

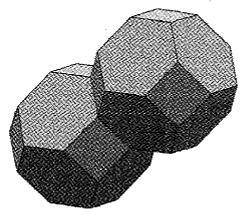
开尔文研究了大约两个多月后，在1887年11月4日，终于找到了答案，如图9所示．这是一个由14个面组成的三维结构球体(tetrakaidecahedron)，其中6个面是4边形，8个面是6边形，被称为开尔文单元(Kelvin cel1)，它按照BCC(body—centered eu—bic)排布，具有高度的对称性．1887年11月20日，开尔文在给Rayleigh的信中说，自己目前正在从事崭新的泡沫结构的研究工作(“⋯I have been in—volved in another affair。··which George Darwin charac—terises as utterly froth⋯ ”)．

图9 采用Surface Evolver软件复现的开尔文单元结构

图10是开尔文发表的论文扉页，在这篇论文中，他明确提出了空间最优排布的猜想，以及他发现的单元结构[6]。

开尔文单元结构是最优美、最对称的三维单元结构之一，尽管一直没有得到证明，但是一个多世纪以来得到了数学家们的认可．1952年，美国数学家Hermann Weyl在他的《Symmetry}一书中首次表示开尔文结构是正确的，没有给出相关的数学证明。

图10 开尔文于1887年提出开尔文猜想的论文第一页

4 Surface Evolver和Weaire—Phle1an结构

Kenneth Brakke是美国Susquehanna University数学系几何中心的教授(见图11)．他于1992年发明了计算最小能量液膜形态的软件“Surface Evol—ver”[7]

它能够数值求解液膜的Gauss-Laplace方程，演化液膜形状．由于该方程是非线性偏微分方程，在绝大多数情况下，没有数值解，Surface Evolver软件则成为最终解决方案；它可以方便直观地进行图形演示和输出，易于使用．在Surface Evolver软件中，液膜被离散为若干微小三角形网格，可以处理复杂拓扑结构，比如4个柏拉图通道构成的交互点(junction)；在给定初始形状下，采用共轭梯度方法寻求最小能量的状态(见图12)，在这里能量可以为表面能、重力势能，也可以根据实际情况自行定义能量；在处理边界时，可以方便地人为设定，比如研究重力作用下不同接触角对应的液滴形状时，接触角依据实际情况输入。

Surface Evovler软件大大促进了物理学家和数学家对空间最优结构的探索进度，并由此得到了更优的泡沫结构．另外，该软件已经用于泡沫动力学的研究，比如二维泡沫的剪切形变和内部拓扑变化等，还应用于空间泡沫材料、生物细胞结构等科学前沿的研究中．英国皇家学会院士、伦敦大学教授

图11 美国Susquehanna大学数学系教授Kenneth Brakke

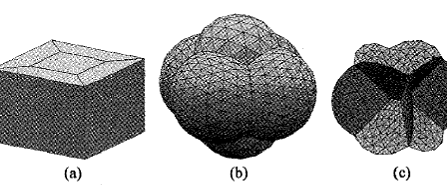
图12 采用Surface Evov[cr软件模拟得到的6个气泡最小表面积时的堆积形态，此时仅考虑表面能(a)初始形态；(b)气泡堆积外表面形态；(c)气泡间的薄膜、柏拉图通道和交汇点

Alan L．Mackay这样评价Surface Evolver软件：“The evolver is a spectecular example of the effects of a gift to science which advances a whole field．”（“E-volver软件推动了整个泡沫领域的科学研究，这在科学研究中是非常突出的例子．”)

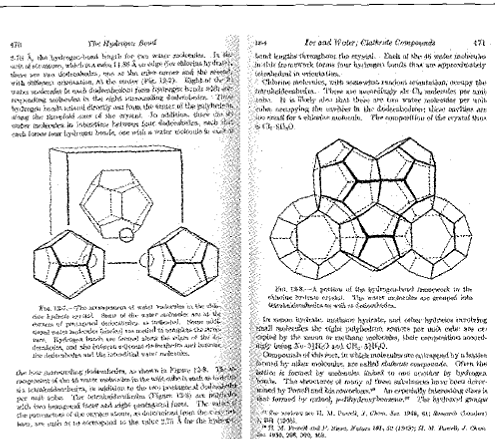
一个典型的例子就是Wearire和Phelan[8] 采用Surface Evovler软件发现了一种新的Weaire-Phe-lan(WP)结构单元，见图13．他们在探索泡沫结构时，把目光转向化学包合物(clathrate)．化学包合物是一种特殊类型的化合物，由分子被包在晶体结构的空腔或大分子固有的空腔中形成．各组分间按一定的比例结合，但不是靠化学键力而是靠组分间的紧密吻合，使较小的分子不致脱离．比如化合物Na₈Si₄₆有8个钠原子被包在晶体结构的空腔中，而晶体结构的节点是46个硅原子．分析表明，这一结构服从柏拉图结构平衡法则．另外，实验检测也证明，Na₈Si₄₆ 的这种排布具有很小的面积，一个Na₈Si₄₆分子有8个格子，其中6个是十四面体，2个是十二面体。

利用这样的化合物分子作为结构模型，Weaire和Phelan采用Brakke开发的Surface Evolver软件进行计算，发现了WP结构单元，它具有两种体积相等、但形状不同的气泡单元：一个是正十二面体(do-decahedron)，另外一个是十四面体(tetrakaidecahe-dron)(其中包括2个六边形和l2个五边形)，见图14．在同等体积时，WP单元结构面积比开尔文单元结构的面积少0．3％ ，这在数学上有重要的意义．WP单元结构是由两个不同的气泡构成的，而开尔文单元结构是一个气泡，目前尚没有严格的数学证明WP结构是最优的，或者开尔文单元是最优的单气泡，估计这需要相当长的时问．

另外，自然界还有很多包合物，具有不同的结构．对它们的细致分析有可能发现更优的结构，但是对他们进行挑选和分析，需要花大量的时问．Hales认为：“I suspect that it will be 20 years or more beforethis question is finally resolved”(“我认为要解决这个问题至少要花2O年的时间”)。

图13 1993年Denis Weaire和Robe-Phelan在一起

图14 不同视角时的Weaire—Phelan结构，WP结构的对称性远不如开尔文单元结构

Brakke回顾说，他错过了发现Weaire-Phelan结构的好机会．早在1960年Linus Pauling出版的书《Nature of the Chemical Bond))(第三版，康乃尔大学出版社)，就已经明确指出了化合物Na₈ Si₄₆ 具有一特定晶体结构，也就是1993年Weaire和Phelan发现的WP结构，见图15．Brakke说这本书就在距他办公桌不到10英尺的书架上，一躺就是10年，而他却浑然不知．他从1991年开始在这本书的旁边孜孜以求，试图突破开尔文单元结构．后来他说如果当时偶然看到这本书的第471页Na₈Si₄₆的晶体结构时，很可能会早于Weaire和Phelan发现这一结构。

与1967年采用柏拉图猜想设计蒙特利尔世博会的德国馆一样，2003年8月，由中国建筑工程总公司、中建国际(深圳)设计顾问有限公司、澳大利

图15 Linus Pauling的书《Nature of the Chemical Bond}(第三版，1960年Cornell大学出版)的第471页已经明确指出包合物Na₈Si₄₆的晶体结构，这就是1993年Weaire和Phelan发现的结构单元

亚PTw公司及ARUP公司四家公司组成的设计联合体中标的“水立方”方案中，幕墙和屋面全部采用Weaire—Phelan单元结构．水立方将是2008北京奥运会水上项目的主要比赛场馆，也是我国的国家游泳中心，能容纳17000名观众．2006年底外层膜结构顺利完工，转入内部设备安装和装修阶段，总预算造价是10亿人民币．膜材料采用乙烯-四氟乙烯共聚物(Ethylene Tetrafluoroethylene，ETFE)材料，它具有抗划伤、不易燃以及抗冲击等优点，可以防范北京的沙尘暴、地震以及其他可能的恶劣自然环境，ETFE膜透光率可高达95％ ，结合稀疏的泡沫骨架，足以保证游泳中心内部自然光充足．内外立面膜结构共由3065个气枕组成(其中最小的l-2m²，最大的达到70m²)，覆盖面积达到10万m²，展开面积达到26万m²，将成为世界上最大的ETFE工程．水立方同时也成为单个气枕最大、拥有内外两层气枕结构的独一无二的建筑物，见图16．由于采用Weaire-Phelan单元结构分割空间，水立方因此成为世界上技术难度最大、最复杂的膜结构工程项目，水立方幕墙工程从分析、设计到施工都是极富挑战性的工作 ．

图16 水立方的骨架结构，其间将镶嵌ETFE膜气枕；右侧图是铺设好ETFE气枕后的水立方外景(摄于2007年春)

5 泡沫动力学

自1970年后，泡沫动力学的研究逐渐被重视起来．一方面受益于相关学科的发展，比如流体力学、微观显像技术和计算技术，另一方面是材料科学和工业生产的驱动，比如航空航天材料需要轻质、高强度的泡沫材料，而泡沫材料内部结构均匀是最关键的，同时在工业生产，不管是希望消除泡沫(比如化工中)还是保留泡沫(比如泡沫灭火剂)，泡沫稳定性的控制是关键，这样就大大促进了泡沫动力学的研究．

泡沫动力学的研究主要涉及渗流(foam drain-age)、粗化(bubble coarsening)、液膜破裂(film rupture)和流变性能等方面，每个方面都很艰难．液态泡沫是一个非平衡系统，表现为它的结构随着时间发生演化，一般涉及三个机制：(1)重力作用下气泡间的液体渗出，使得气泡与液体分离，称为泡沫渗流；(2)气泡间液膜的破裂造成相邻气泡合并，称为液膜破裂；(3)分子通过液膜从内部高压强的小气泡中向相邻低压强的大气泡扩散所造成的气泡合并，称为气泡粗化．在以上三个非平衡机制中，气体扩散过程比较缓慢，液膜破裂可以采用合适的表面活性剂予以消除，重力驱使的泡沫渗流则不可避免，直接影响泡沫稳定性，因而泡沫渗流的调控具有明确的应用价值和理论意义．这三个机制又相互关联：当渗流发生时，液膜内微量液体的流动会影响气泡间的气体扩散；同时液膜破裂和气体扩散过程导致气泡平均直径增加，又会加快微量液体渗流．这三种机制相互关联，使得液态泡沫呈现出随时间不断变化的非平衡特性．目前，人们对于这些影响泡沫稳定性的机制没有完全了解．

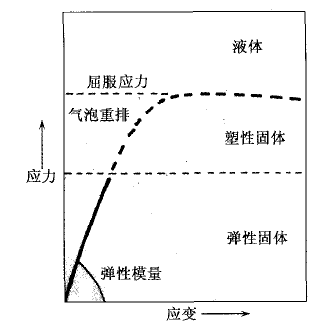
液态泡沫的独特流变特性如图17所示，在常规重力或较小外力下，不足以使得液态泡沫流动，此时液态泡沫就像固体，具有一定的弹性．泡沫的剪切模量来自液膜表面张力，与气泡大小和液体体积分数有关，一般在10Pa的量级，相比之下钢的剪切模量为8×10 Pa．当形变较大时，部分气泡问发生拓扑变化，当应力逐渐消去时，这种拓扑变化不会复原，

图17 液体泡沫应变系示意图泡沫发生塑性变形．如果应力继续增大并超过屈服应力值时，泡沫内发生大量拓扑变化，泡沫开始流动．

1999年，Weaire和Hutzler [10泡沫物理学专著(The Physics of Foams>，成为继柏拉图所著的《Statique Expeimentale et Therique des Liquides soumis aux Seules Forces Moleulaires)之后的另一本标志性著作，见图18．{The Physics of Foams}不仅总结了泡沫静力学和结构方面的最新研究进展，而且用一半篇幅来介绍泡沫动力学方面的最新工作．该书自出版以来得到了众多著名科学家的高度评价，比如：法国物理学家P．G．de Gennes[11](1933-007，1991年物理学诺贝尔奖获得者)的评价：“⋯the book represents a major advance．It is written in a pleasant style and is accessible to a wide population of physicists．”(“⋯⋯这本书标志了一个重大的进步．书的内容深入浅出能为绝大多数物理学家读懂”)；

英国物理学家G．C．Barker[12]是：“⋯the authors coherent account will benefit researchers at all levels．In addition，Physics of Foams includes man—Y beautiful photographs and computer——generated i11us—trations of foam structures．．．that will ensure the con—tinued fascination of all readers．”(“⋯ ⋯作者连贯的阐述有益于不同水平的研究人员．此外，这本书中还有很多漂亮的图片以及一些用电脑生成的泡沫结构插图⋯⋯这些将必然引起读者强大的兴趣”)．

著名的国际会议“European Conference on Foams，Emulsions and Applications(EUFOAM)”从1994年开始每两年召开一次，参会人员来自涉及泡沫的各个领域，规模也越来越大，每一次会议的主题都在做相应改进．早在1994年，Weaire邀请了泡沫物理学界在爱尔兰西海岸的小村庄Renvyle开会．

图18 Weaire和Hutzler写的泡沫物理学专著，由牛津大学出版社1999年出版．右图是作者Hutzler和Weaire在新书发布时的合影

这应该是国际上第一次关于专门讨论泡沫结构及性能的会议，参会人员包括物理学家、数学家、化学家以及来自工业界研发中心的专家，当时规模并不大，只有50人左右，是Weaire精心选出的．他们都分别从各自角度汇报了研究进展，讨论泡沫中遇到的共同感兴趣的问题．当时，大家一直要求两年后再开一次会议．1996年，在法国南部的海滨城市Arcachon召开了第二次会议，前两次召开会议时没有固定的会议名称．之后名称正式定下来：European Conference on Foams，Emulsions and Applications，并约定每两年一次，简称EUFOAM，而没有采用EURO-FOAM，这是由于奥地利一家生产塑料泡沫的大公司(http：//www．Euro-foam．com)在几年以前就已经注册了EUROFOAM 商标．2000年，在荷兰的TU Delft大学召开了第三届；2002年在英国曼彻斯特理工大学(UMIST)召开了第四届；2004年在法国巴黎南部的University of Marne-la-Vallée召开了第五届．2006年，在德国的波茨坦(Potsdam)的马普学会Max Planck Institut Colloids and Interfaces召开了第六届．在这次会上，来自24国家的190多位科学工作者参加了这次会议．第七届EUFOAM会议将于2008年7月，由位于荷兰西南部海滨小镇Noordwijk的欧洲航天总署(the European Space Agency，ESA)研发中心主办．ESA是一直积极促进和资助欧洲泡沫物理的研究工作，特别是微重力下泡沫稳定性的研究．EUFOAM会议涉及泡沫研究的方方面面，根据目前较为活跃的研究工作，一般可以列为8个主题：液体界面和液膜的几何表征，泡沫和乳液的物理机制，泡沫和乳液稳定性和失稳的控制，液体界面层、液膜、泡沫和乳液的流变性能，液膜、泡沫和乳液内在性能参数间的关联，新实验技术，微重力在泡沫和乳液中的应用，工业过程及应用.

6 结束语

泡沫物理学在历史长河中艰难的行走了近两个世纪，柏拉图和开尔文等伟人的光芒照耀了我们前行的路，泡沫动力学的研究是我们所要力攻的堡垒．现有的物理理论和实验检测等诸多方面都还不完整，巴黎第七大学的(Université Paris Diderot-Paris 7)Wiebke Drenckhan曾形象地说：“this subject is still in its infancy”(“这门学科仍处于幼年时期”)．

在国内，泡沫物理的研究寥若晨星，只有少数文献报道了关于泡沫材料制备工艺控制和多孔介质渗流等的工业应用研究，报道研究的角度多为在泡沫材料及多孔介质内流动的物质本身的物理化学性质以及环境宏观性质(如温度、压力等)对渗流的影响，对材料结构的基础理论研究报道并不多。

泡沫流变特性和渗流的研究是目前和今后很长一段时间内的研究热点[13]，利用多尺度方法，在整个泡沫对应的宏观尺度检测液体渗流，验证和改进现有的理论；在多气泡的介观尺度(因为泡沫中的拓扑变化主要发生在局部)观测泡沫中微流动引起的气泡协调变形甚至拓扑变化；在单气泡微观尺度分析渗流时柏拉图通道和交汇点的位移，以及探索非常规重力环境下的泡沫体系的结构和力学特性演变等方面，加强泡沫渗流机理的理论和实验研究将是我们追赶国际水平的一个很好的切入点．

参考文献

[1] 孙其诚，黄晋．物理，2006，35：1050[SunQ C，Huang J．Wuli (Physics)，2006，35：1050(in Chinese)]

[2] Plateau J A F．Statique Expérimentale et Théorique des Liquides Soumis allx Seules Forces Moléculaires．Paris：Gauthier Viliars，1873

[3] Hutzler S，Weaire D，Cox S J et a1．Europhys Lett．，2007，77：28002

[4] Ed．Weaire D．The Kelvin Problem．Foam Structures of Minimal Surface Area．London：Taylor＆ Francis．1997

[5]Maxwell J C．Nature，1874，10：119

[6] Thomson W，Lord Kelvin．Phil Mag．，1887，24：503

[7] Brakke K．Exp Math．，1992，1：141

[8] Weaire D，Hutzler S．The Physics of Foams．England：Oxford University Press，1999

[9] Ball P．Nature，2007，448：256

[10] Weaire D，Phelan R．Phil Mag Lett．，1994，69：107

[11] Weaire D，Hutzler S．Physics Today，2001，54(3)：54

[12] Barker G C．Science，2000，289：398

[13] 黄晋，孙其诚．力学进展，2007，37：269[Huang J，Sun Q C．Advances in Mechanics．2007，37：269(in Chinese)