织物层热湿传递过程仿真研究

郑连锋 张洪弟 (青岛大学 266071)

原载：《北京纺织》2004/No5;48-51

收稿日期：2004-05-17

作者简介：郑连锋(1979-)男，青岛大学纺织系2001级研究生，从事纺织新材料、新工艺、新设备的研究。

〖摘要〗 对服装织物层基本几何单元内空气层与纱线热湿传递机理模型进行了数值模拟分析，建立了空气层与纱线交界处的热湿传递动态过程，通过计算机仿真分析了织物内纱线、空气层的温度场和湿度场，并探讨了纱线材料特性、织物的组织结构对织物层热湿传递过程的影响规律。

〖关键词〗织物;仿真分析;热湿传递

中图分类号:T5101·92⁺3.2-3.6 文献标识码:A 文章编号:1002-3348(2004)05-0048-04

在人体-服装-环境这一系统中，人体产生的热量与湿度通过微小气候，经服装层传向外部环境。织物层的热湿传递过程直接影响人体的舒适性，故织物层的热湿传递研究非常重要。目前大部分学者主要致力于进行织物层热湿传递过程的实验模拟研究[1,2]，由于织物层厚度小，无法准确测量织物内部温度场和湿度场，故研究结果只能获取一些宏观数据，往往不具有推广应用价值。另外，近几年已有部分学者将人体、环境、服装结合起来，通过计算机对该过程进行动态模拟[3,4]，但是所采用的模型考虑因素不够全面，许多问题需进一步深入研究；鉴于此，本文以织物层为研究对象，并通

过仿真分析织物内部微观的热湿传递过程，获得一系列有用的，实验无法测量的数据。

1 热湿传递理论模型

1·1热湿传递物理模型

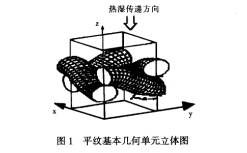
以织物几何单元 (包含纱线和纱线间空气)为研究对象，图1给出了平纹基本几何单元立体图(图中热湿传递方向为织物厚度方向)

1·2热湿传递数学模型

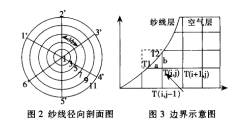
织物层的传热传湿是包含纱线和纱线间空气传热传湿的复杂过程，而纱线和空气的传热传湿特性是不同的，因此我们对其分别研究。在其交界处，考虑到纱线的弯曲，对其边界条件做了处理。此处的边界为不规则边界[5](图3)，由于我们在空气层和纱线层采用不同的坐标系统，纱线层我们采用柱面坐标，图2所示为纱线轴向某一断面结构图；而空气层采用直角坐标。我们在计算纱线层边界温湿度时，利用空气层传入的热湿流作为边界条件，在计算空气层温度时利用 《传热学》中边界节点方程式来求解。

图中箭头所示的空气层节点，如图3(i,j)点，空气层边界处有很多这样的点，它们分别被纱线包含一个点、两个点、三个点，图3所示点为被纱线包含三个点的情况，计算公式[6]；

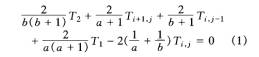
对空气层内部节点利用质量、能量守恒建立热湿传递数学模型:

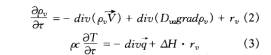
对纱线内部节点应用动量和能量守恒得到其湿分和温度的数学表达式。本文采用已建立的热湿传递数学模型:

热传递数学模型:

湿传递数学模型:

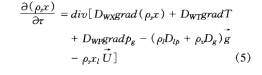
2 理论模型的仿真分析

我们对上面建立的数学模型采用完全隐式差分格式进行三维离散，用MATLAB语言编制程序进行模拟计算，并运用MATLAB作图工具把计算出的数据通过图形清晰的显示出来，然后加以定性分析。

2·1本色纯棉细平布的仿真分析

对织物C155(19.5×19.5(tex)×3ll×318.5)进行了模拟研究，工况：设其在温度为20℃，相对湿度为20%的空气中达到平衡，后置于一侧温度为22℃，相对湿度为40%，另一侧温度为20℃，相对湿度为20%的空气中。

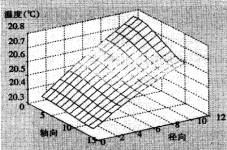
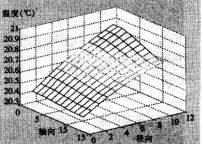
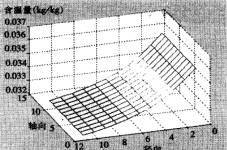
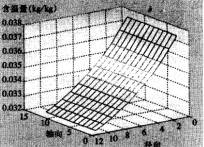
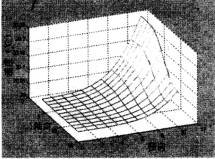
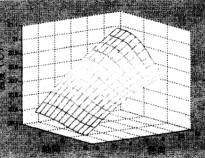
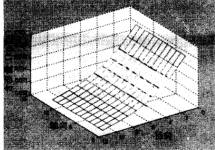
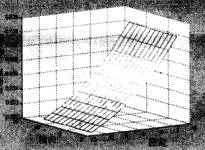
由图4、5、6、7可知，热湿传递开始后，纱线外侧与空气的边界处由于温度高且湿度大，热量和湿分开始由高温高湿面向低温低湿面传递。热量的传递及湿分的凝结使得织物内侧附近节点温度、湿度迅速升高，而距离边界较远的纱线中心节点则因为受其影响较小，温度、湿度变化幅度相对较小。纱线表面节点受纱线间空隙温、湿度影响比纱线轴心节点大，因而其初始时刻温、湿度值都比纱线轴心节点大。

图4 2秒时的温度分布	图5 15秒时的温度分布
图6 2秒时的含湿量分布	图7 15秒时的含湿量分布

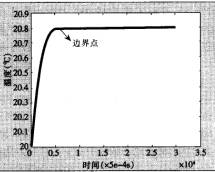
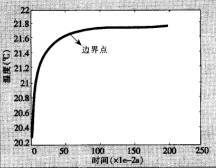
由图8、9的对比可以看出，纱线间空气的传递过程较为迅速，而纱线的传递过程较纱线间空气的平衡过程长的多，由图8、9可以很明显的看出，纱线间空气在很短的时间就达到了平衡，这是因为纱线间隙的总压差促使空气运动，从图8、

9可以看出吸热与时间的关系形成对数曲线，所以从理论上来说，达到真正平衡的时间，实际上是无限长的。在闷热的夏天，人们穿着稀薄 (孔隙率大)的织物，人体表面产生的气态汗可以较快传递出去，在很大程度上降低了人体出汗时的闷热感，故有凉爽的感觉；在寒冷的冬天，人们穿着致密厚实 (孔隙率小)的织物，以防止冷空气进入微小气候以及人体产生的热量通过服装迅速的散发出去。

图8 纱线内温度随时间变化	图9 纱线间空气温度随时间分布

2·2 斜纹织物热湿传递仿真分析

我们对上述织物材料应用于不同的组织结构中，纱线的细度、经纬密度不变，我们得到了1/2斜纹组织的热湿传递规律。

图10 1秒时的温度分布	图11 15秒时的温度分布
图12 1秒时的含湿量分布	图13 15秒时的含湿量分布

从图10、11、12、13可以看出，轴向温度的分布规律和纱线的弯曲方向是相关的。在经纬密度、细度相同的条件下，经纬纱交织次数越多，织物结构较为紧密 (相对斜纹织物而言平纹交织次数多)，其透气性能较差，热湿传递性能也差，平纹织物的15秒温度值最大为20.82℃，含湿量为0.037kg/kg;而斜纹织物在15秒时温度20.98℃，含湿量为0.038kg/kg。我们可以将原因归结为空气在织物几何单元中的比例，即孔隙率。孔隙率大的织物在热湿传递过程中，空气的作用比孔隙率小的织物作用大，因而其热湿性能好。

通过以上两种情况的讨论和比较，我们同样可以得到:织物的结构，主要包括纱线的位置及弯曲方向等，决定了织物在热湿传递过程中的分布规律。织物的结构对热湿传递的影响至关重要，织物中纱线的弯曲是产生轴向温差的主要原因，开始时的分布规律与纱线的形状关系较为明显:随着传递的进行，轴向的差距减小;热湿传递的差别完全可以从结构上的差别得到预测。我们可以设想如果织物组织结构是不同于平纹及斜纹的，而是其它较为复杂的织物结构，也可以在分析织物中纱线与孔隙的位置关系的基础上，大致推断出其热湿分布规律。

3 结论

本文利用己经建立的服装层热湿传递理论模型，利用双坐标系统对纱线和纱线间空气的热湿传递情况进行了仿真分析可以得到以下几点规律:

(1)纱线平衡所需时间远大于空气平衡所需时间，所以空隙率大的织物热湿传递性能好；

(2)织物中纱线的空间位置、弯曲方向对织物的热湿分布规律产生了很大的影响，可以由此预测较为复杂组织结构织物的热湿分布规律。

参考文献

[1]蒋培清，服装热湿舒适性研究方法综述[J]丝绸，1998(11)；42-44

[2] Rene M. Rossi, Rene Gross. Water Vapor Transfer and Condensation Effects in Multilayer Textile Combinations [J] Textile Research Journal 2004,74(1); 1-5

[3] T. Nishimura, T. Matsuo. Numerical Simulation of Moisture Transmission Through a Fiber Assembly [J] Textile Research Journal 2001,70 (2); 103-107

[4]李风志等，织物热湿传递机理模型研究[J]大连理工大 学学报，2003，43(1)28-32

[5]陶文铃，数值传热学[M]西安:西安交通大学出版社，2002

[6]章熙民等，传热学[M]北京:中国建筑工业出版社，1998，79-80